Question

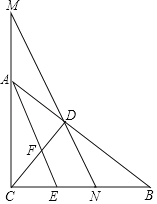
【题目】如图，已知正方形，点是线段延长线上一点，联结，其中．若将绕着点逆时针旋转使得与第一次重合时，点落在点(图中未画出)．求：在此过程中，

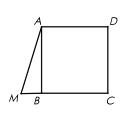
（1）旋转的角度等于 ______________．

（2）线段扫过的平面部分的面积为__________(结果保留)

（3）联结，则的面积为____________．

Answer 1

【答案】90； ； 5

【解析】

(1)根据旋转角的定义即可求得答案；
(2)由题意得，线段扫过的平面部分的面积为扇形ABD的面积，再根据扇形的面积公式求解即可；

(3)先利用勾股定理求出AN的长，再求的面积即可.

解：(1) ∵已知正方形，

∴∠BAD=90°,

∴将绕着点逆时针旋转使得与第一次重合时，旋转的角度等于90°,

故答案为90.

(2)如图，

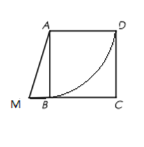
∵线段扫过的平面部分的面积为扇形ABD的面积，,

∴S扇形ABD=××32=,

故答案为.

(3)如图，

∵旋转变换的性质知，AD=AB=3,DN=MB=1,

∴AN= = ,

∵∠MAN=90°,

∴S△MAN=××=5,

故答案为5.