Question

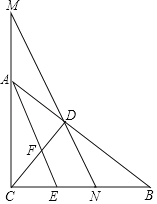
【题目】如图，Rt△ABC中，∠ACB=90°，斜边AB边上的高CD与角平分线AE交于点F，经过垂足D的直线分别交直线CA，BC于点M，N．

（1）若AC=3，BC=4，AB=5，求CD的长；

（2）当∠AMN=32°，∠B=38°时，求∠MDB的度数；

（3）当∠AMN=∠BDN时，写出图中所有与∠CDN相等的角，并选择其中一组进行证明．

Answer 1

【答案】（1）CD；（2）∠MDB=160°；（3）与∠CDN相等的角有∠AFD，∠CFE，∠AEC，∠MNC；证明见解析．

【解析】

（1）根据三角形面积公式即可得到结论；

（2）根据三角形的内角和定理求出∠MNC，进而得出∠MNB，再利用三角形外角的性质即可得到结论；

（3）首先根据角平分线的定义和平行线的判定和性质证明AE∥MN，然后结合同角的余角相等可证明所有结论．

解：（1）在Rt△ABC中，∠ACB=90°，

∴S△ABCACBC3×4=6．

∵CD是斜边AB上是高，

∴S△ABCABCD5×CD=6，

∴CD；

（2）∵∠ACB=90°，∠AMN=32°，

∴∠MNC=180°﹣∠ACB﹣∠AMN=58°，

∴∠MNB=180°﹣∠MNC=122°，

∴∠MDB=∠MNB+∠B=122°+38°=160°；

（3）与∠CDN相等的角有∠AFD，∠CFE，∠AEC，∠MNC；

理由：∵∠AMN=∠BDN，∠BDN=∠ADM，

∴∠AMN=∠ADM，

∴∠CAB=∠AMN+∠ADM=2∠AMN，

∵AE是∠CAB的角平分线，

∴∠CAB=2∠CAE，

∴∠AMN=∠CAE，

∴AE∥MN，

∴∠CDN=∠AFD=∠CFE，

∵∠ACB=90°，

∴∠AMN+∠MNC=90°，

∵CD⊥AB，

∴∠BDN+∠CDN=90°，

∵∠AMN=∠BDN，

∴∠CDN=∠MNC，

∵AE∥MN，

∴∠AEC=∠MNC，

∴∠CDN=∠AEC．