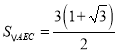Question

【题目】如图，在平面直角坐标系中，一次函数y＝x﹣2的图象分别交x、y轴于点A、B，抛物线y＝x2+bx+c经过点A、B，点P为第四象限内抛物线上的一个动点．

（1）求此抛物线的函数解析式；

（2）过点P作PM∥y轴，分别交直线AB、x轴于点C、D，若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似，求点P的坐标；

（3）当∠PBA＝2∠OAB时，求点P的坐标．

Answer 1

【答案】（1）；（2）点P的坐标是（，﹣5）或（，﹣2）；（3）点P的坐标是（3，）．

【解析】

（1）本题所求二次函数的解析式含有两个待定字母，一般需要两个点的坐标建立方程组，现在可求A、B点坐标，代入列方程组可解答；

（2）根据∠ADC＝90°，∠ACD＝∠BCP，可知相似存在两种情况：

①当∠CBP＝90°时，如图1，过P作PN⊥y轴于N，证明△AOB∽△BNP，列比例式可得结论；②当∠CPB＝90°时，如图2，则B和P是对称点，可得P的纵坐标为﹣2，代入抛物线的解析式可得结论；

（3）设点A关于y轴的对称点为A′，求出直线A′B的解析式，再联立抛物线的解析式解答即可．

解：（1）令x＝0，得y＝x﹣2=-2，则B（0，﹣2），

令y＝0，得x﹣2=0，解得x＝4，

则A（4，0），

把A（4，0），B（0，﹣2）代入y＝x2+bx+c（a≠0）中，

得解得．

∴抛物线的解析式为：．

（2）∵PM∥y轴，

∴∠ADC＝90°．

∵∠ACD＝∠BCP，

∴以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似，存在两种情况：

①当∠CBP＝90°时，如图，过P作PN⊥y轴于N，

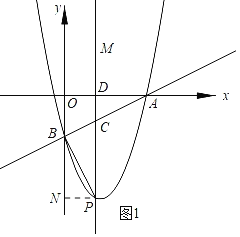
∵∠ABO+∠PBN＝∠ABO+∠OAB＝90°，

∴∠PBN＝∠OAB，

∵∠AOB＝∠BNP＝90°，

∴Rt△PBN∽Rt△BAO．

∴=.

设P(x,x2-x-2)．

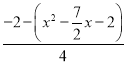∴=，化简,得x2-x=0．

解得x＝0（舍去）或x=．

当x=时，y=x2-x-2=-5.．

∴p(，﹣5）；

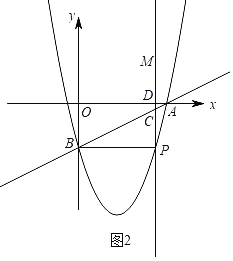
②当∠CPB＝90°时，如图2，则PB∥x轴，所以B和P是对称点．

所以当y＝﹣2时，即x2-x-2=-2，解得x＝0（舍去）或x=．

∴P(，﹣2）．

综上，点P的坐标是（，﹣5）或（，﹣2）．

（3）设点A关于y轴的对称点为A′，则A′B＝AB．

∴∠BAO＝∠B′AO．

直线A′B交抛物线于P．

∴∠PBA＝∠BAO+∠BA′O＝2∠BAO．

∵A（4，0），

∴A′（﹣4，0）．

设直线A′B的解析式为y＝kx+b（k≠0）．

∵B（0，﹣2）．

∴

解得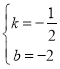

∴直线A′B的解析式为y=x-2．

由方程组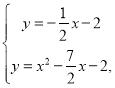得x2﹣3x＝0．

解得x＝0（舍去）或x＝3．

当x＝3时，y=x-2=-．

所以点P的坐标是（3，）．