题目内容
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,以
,以![]() 为边向外作等边
为边向外作等边![]() ,连接
,连接![]() 交
交![]() 于
于![]() 若点
若点![]() 为
为![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,连接
,连接![]() 且
且![]() 平分
平分![]() ,下列选项正确的有( )
,下列选项正确的有( )
①![]() ;②
;②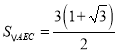 ;③
;③![]() ;④
;④![]()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】C
【解析】
①连结OE,根据正方形性质和等边三角形性质可证:OE垂直平分AD,进而可证:△CDF∽△EOF,由相似三角形性质即可求得DF;
②由![]() ,又由两条平行之间的距离处处相等得
,又由两条平行之间的距离处处相等得![]() ,即可得
,即可得![]() ,利用三角形面积公式计算即可得出结果;
,利用三角形面积公式计算即可得出结果;
③过点F作PQ⊥CD分别交CD、AB于点P、Q,在MA上截取MT=MC,连接FT、CT,求得相关的线段长,可证:△MCF≌△MTF(SAS),Rt△CFP≌Rt△FTQ(HL),求出BT的长,利用特殊角的三角函数值和等边三角形的判定与性质即可求得![]() ;
;
④根据解直角三角形和线段的加减运算分别求出![]() 的长,整理即可得出这三条线段之间的数量关系,即可做出判断.
的长,整理即可得出这三条线段之间的数量关系,即可做出判断.
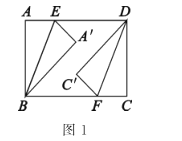
解:如图1,连结OE,

∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠ADC=∠DAB=90°,OD=OB,OC=OA,BD=AC,
∴OD=OB=OC=OA,
∵△ADE是等边三角形,![]() ,
,
∴![]() ,∠ADE=60°,
,∠ADE=60°,
∴![]() ,
,
∴![]() ,
,
则![]() ,
,
∵AE=DE,OD=OA,
∴OE垂直平分AD,即OE⊥AD,DH=AH![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∵∠ADC=∠DHE=90°,
∴CD∥OE,
∴△CDF∽△EOF,
∴![]() ,则
,则![]() ,即
,即![]() ,
,
∵![]() ,则
,则![]() ,
,
∴![]() ,解得:
,解得:![]() ,故①正确;
,故①正确;
∵![]() ,
,
又∵CD∥OE,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() ,
,
故②正确;
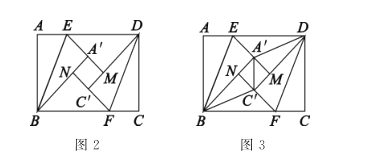
如图2,过点F作PQ⊥CD分别交CD、AB于点P、Q,在MA上截取MT=MC,连接FT、CT,则![]() 为等腰三角形,
为等腰三角形,
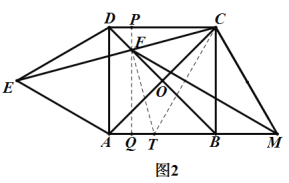
在![]() 中,
中,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
由![]() 得:
得:![]() ,则
,则![]() 为等腰直角三角形,
为等腰直角三角形,
∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,
∴![]() ,则
,则![]() ,
,
![]() ,
,
∵FM平分∠AMC,
∴∠CMF=∠AMF,
在△MCF和△MTF中,
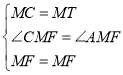 ,
,
∴△MCF≌△MTF(SAS),
∴CF=FT,
在Rt△CFP和Rt△FTQ中,
![]()
∴Rt△CFP≌Rt△FTQ(HL),
∴![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,则
,则![]() 为等边三角形,
为等边三角形,
∴![]() ,故③正确;
,故③正确;
∵![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]() ,
,
∵![]()
∴![]() ,故④错误;
,故④错误;
∴正确的选项有3个,
故选:C.

 寒假学与练系列答案
寒假学与练系列答案