题目内容
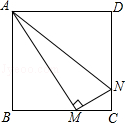
正方形ABCD的边长为1cm,M、N分别是BC.CD上两个动点,且始终保持AM⊥MN,当BM= cm时,四边形ABCN的面积最大,最大面积为 cm2.

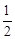 ,
, 。
。设BM=xcm,则MC=1﹣xcm,
∵∠AMN=90°,∠AMB+∠NMC=90°,∠NMC+∠MNC=90°,∴∠AMB=90°﹣∠NMC=∠MNC。
∴△ABM∽△MCN,∴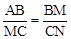 ,即
,即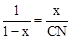 ,解得CN=x(1﹣x)。
,解得CN=x(1﹣x)。
∴ 。
。
∵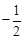 <0,∴当x=
<0,∴当x=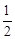 cm时,S四边形ABCN最大,最大值是
cm时,S四边形ABCN最大,最大值是 cm2。
cm2。
∵∠AMN=90°,∠AMB+∠NMC=90°,∠NMC+∠MNC=90°,∴∠AMB=90°﹣∠NMC=∠MNC。
∴△ABM∽△MCN,∴
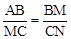 ,即
,即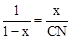 ,解得CN=x(1﹣x)。
,解得CN=x(1﹣x)。∴
 。
。∵
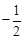 <0,∴当x=
<0,∴当x=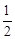 cm时,S四边形ABCN最大,最大值是
cm时,S四边形ABCN最大,最大值是 cm2。
cm2。
练习册系列答案
相关题目

 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
 的方程:
的方程: ①和
①和 ②,其中
②,其中 .
. 的图象与
的图象与 、
、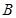 两点(点
两点(点 处,点
处,点 处,若点
处,若点 的值;
的值; ,在(2)的条件下,函数
,在(2)的条件下,函数 ,
, 的图象位于直线
的图象位于直线 (
( )交于两点,当向上平移直线
)交于两点,当向上平移直线 的值是________________.
的值是________________.
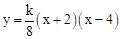 (
(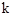 为常数,且
为常数,且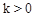 )与
)与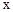 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与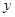 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线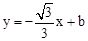 与抛物线的另一交点为D.
与抛物线的另一交点为D.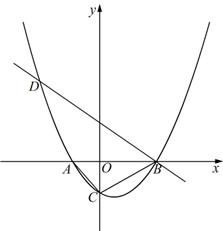
 的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC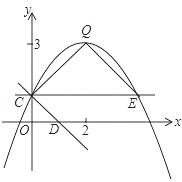
 的图象与x轴有两个公共点,那么一元二次方程
的图象与x轴有两个公共点,那么一元二次方程 有两个不相等的实数根.”据此判断方程x2-2x=
有两个不相等的实数根.”据此判断方程x2-2x= -2实数根的情况是 ( )
-2实数根的情况是 ( )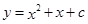 的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是
的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是