题目内容
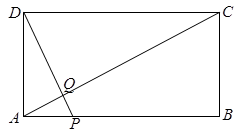
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位的速度向B点移动,移动时间为t秒.
①当t为何值时,DP⊥AC?
②设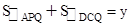 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位的速度向B点移动,移动时间为t秒.
①当t为何值时,DP⊥AC?
②设
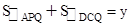 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
(1)证明见解析;(2)①5;②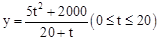 ,8-9.
,8-9.
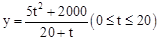 ,8-9.
,8-9.试题分析:(1)如图,由矩形的性质求出∠1=∠2,∠3=∠4即可证明△APQ∽△CDQ.
(2)①当DP⊥AC时,由△ADC∽△PAD列比例式可求解.
②根据相似,求出两个三角形的高(用t的代数式表示),即可求出y与t之间的函数解析式;列表求出函数值得出P点运动到第8秒到第9秒之间时,y取得最小值.
试题解析:(1)如图,∵四边形ABCD是矩形,∴AB∥CD. ∴∠1=∠2,∠3=∠4.
∴△APQ∽△CDQ.
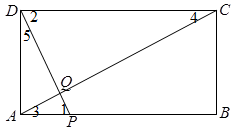
(2)①当DP⊥AC时,∴∠4+∠2=90 o.
又∵∠5+∠2=90 o,∴∠4=∠5.
又∵∠ADC=∠DAP=90 o,∴△ADC∽△PAD.∴
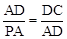 ,即
,即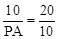 .∴PA=5.
.∴PA=5.∵P点从A点出发沿AB边以每秒1个单位的速度向B点移动,∴t=5.
②设△APQ的边AP上的高为h,则△DCQ的边上的高为
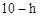 .
.∵由(1)△APQ∽△CDQ,∴
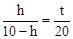 .∴
.∴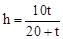 .∴
.∴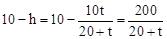 .
.∴
 ,
,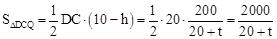 .
.∴
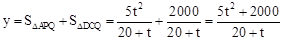 .
.∴y与t之间的函数解析式为
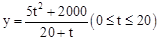 .
.给出t的部分取值,计算出y的对应值列表如下:
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 100 | 95.48 | 91.88 | 88.91 | 86.67 | 85 | 83.85 | 83.15 | 82.86 | 82.93 | 83.33 |
| t | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| y | 84.03 | 85 | 86.21 | 87.65 | 89.29 | 93.11 | 95.26 | 97.56 | 100 | | |
从表中可看出:
当
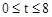 时;y随t的值的增大而减小;当
时;y随t的值的增大而减小;当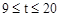 时;y随t的值的增大而增大.
时;y随t的值的增大而增大.∴P点运动到第8秒到第9秒之间时,y取得最小值.

练习册系列答案
相关题目
 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
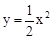 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交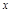 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.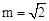 时,求S的值.
时,求S的值.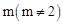 的函数解析式.
的函数解析式.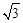 时,求
时,求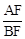 的值;
的值;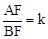 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.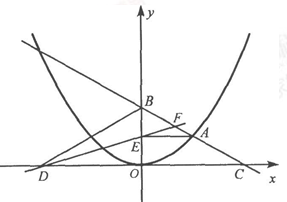
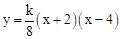 (
(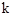 为常数,且
为常数,且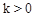 )与
)与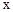 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与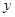 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线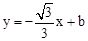 与抛物线的另一交点为D.
与抛物线的另一交点为D.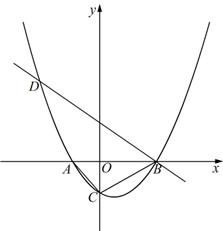
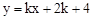 与抛物线
与抛物线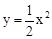 交于A、B两点,
交于A、B两点,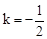 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;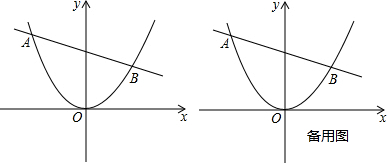
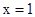 的抛物线的解析式 .
的抛物线的解析式 .
