题目内容
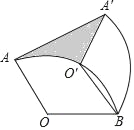
【题目】如图,将半径为6,圆心角为120°的扇形OAB绕点B顺时针旋转60°,点O,A的对应点分别为O′,A′,连接AA′,在图中阴影部分的面积是_____.
【答案】18![]() ﹣6π.
﹣6π.
【解析】
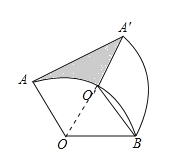
连接OO′,根据旋转的性质得到∠OBO′=60°,推出△OBO′是等边三角形,得到∠BOO′=60°,推出△OO′B是等边三角形,得到∠AO′B=120°,得到∠O′A′B=∠O′BA′=30°,根据图形的面积公式即可得到答案.
连接OO′,
∵将半径为6,圆心角为120°的扇形OAB绕点B顺时针旋转60°,
∴∠OBO′=60°,
∴△OAO′是等边三角形,
∴∠AOO′=60°,OO′=OA,
∴当O′中⊙O上,
∵∠AOB=120°,
∴∠O′OB=60°,
∴△OO′B是等边三角形,
∴∠AO′B=120°,
∵∠AO′A′=120°,
∴∠A′O′B=120°,
∴∠O′A′B=∠O′BA′=30°,
∴图中阴影部分的面积=S△A′O′B-(S扇形O′OB-S△OO′B)=![]() 18
18![]() ﹣6π.
﹣6π.
故答案是:18![]() ﹣6π.
﹣6π.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?