Question

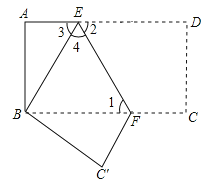
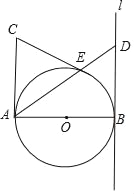
【题目】如图，AB=AC=8，∠BAC=90，直线l与以AB为直径的⊙O相切于点B，点D是直线l上任意一动点，连结DA交⊙O点E．

（1）当点D在AB上方且BD=6时，求AE的长；

（2）当CE恰好与⊙O相切时，求BD的长为多少？

Answer 1

【答案】（1）AE=；（2）BD= 4．

【解析】

（1）连接BE，在Rt△ABD中，利用勾股定理求出AD的长，进而利用直角三角形等面积求出BE的长，在Rt△ABE中，利用勾股定理即可求出AE的长。

（2）连接OC，证明△ABD≌△CAO，根据全等三角形的性质即可求出BD的长.

解：（1）∵AB为直径，

∴∠AEB=90°，

∵BD为切线，

∴AB⊥BD，

∴∠ABD=90°，

在Rt△ABD中，

∵

∴

在Rt△ABE中，

（2）连接OC，如图，

∵∠BAC=90°，

∴CA为⊙O的切线，

∵CE为⊙O的切线，

∴CA=CE，

而OA=OE，

∴OC垂直平分AE，

∴∠1+∠3=90°，

而∠1+∠2=90°，

∴∠2=∠3，

而AB=CA，∠CAO=∠ABD，

∴△ABD≌△CAO，

∴BD=AO=4．