Question

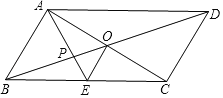
【题目】已知BD是△ABC的角平分线，点E在边AB上，BC＝BE，过点E作EF∥AC，交BD于点F，连接CF．

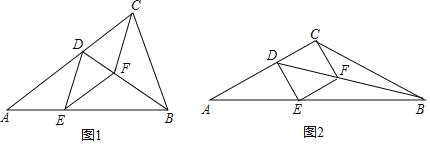
(1)如图1，求证：四边形CDEF是菱形；

(2)如图2，当四边形CDEF是正方形，且AC＝BC时，在不添加辅助线的情况下，请直接写出图中度数等于30°的角．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）直接由SAS得出△BDE≌△BDC，得出DE=DC，∠BDE=∠BDC．再由SAS证明△BFE≌△BFC，得出EF=CF．由EF∥AC得出∠EFD=∠BDC，从而∠EFD=∠BDE，根据等角对等边得出DE=EF，从而DE=EF=CF=DC，由菱形的判定可知四边形CDEF是菱形；

（2）如图2，利用正方形的性质可得∠DFE=45°，然后证明∠FEB=∠CBE=2∠FBE即可．

在△BDE和△BDC中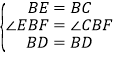，∵，∴△BDE≌△BDC，∴DE=DC，∠BDE=∠BDC．

同理△BFE≌△BFC，∴EF=CF．

∵EF∥AC，∴∠EFD=∠BDC，∴∠EFD=∠BDE，∴DE=EF，∴DE=EF=CF=DC，∴四边形CDEF是菱形；

（2）∵四边形CDEF是正方形，∴∠CDE=∠DEF=2∠EFD=90°．

∵AC=BC，∴∠A=∠CBE．

∵∠A+∠AED=180°﹣90°=90°，∠AED+∠FEB=90°，∴∠A=∠FEB=∠CBE=2∠EBF．

∵∠EBF+∠FEB=∠DFE=45°，∴∠EBF=15°，∴∠FEB=30°，∴∠A=∠ABC=∠FEB=30°．

∵△BFE≌△BFC，∴∠FEB=∠FCB=30°，图中度数等于30°的角是∠A，∠ABC，∠FEB，∠FCB．