题目内容
【题目】在矩形ABCD中,AB=5,BC=12,点A在⊙B上,如果⊙D与⊙B相交,且点B在⊙D内,那么⊙D的半径长可以等于________.(只需写出一个符合要求的数)
【答案】14(答案不唯一)
【解析】
首先求得矩形的对角线的长,然后根据点A在⊙B上得到⊙B的半径为5,再根据 ⊙D与⊙B相交,得到⊙D的半径R的取值范围,再根据圆与圆的位置关系进行解答.
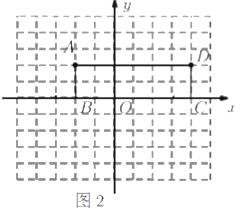
如图,
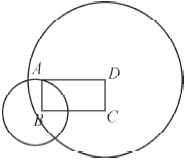
根据矩形的性质和勾股定理,得BD=13,
已知点A在⊙B上,可知⊙B的半径为AB=5,
∵点B在⊙D内,
∴⊙D的半径R>13.
∵⊙D与⊙B相交,
∴圆心距=BD=13,
∴R-5<13<R+5,
∴8<R<18.
综上所述可知13<R<18,从中选一个数填写即可.
∴14符合要求.
故答案为:14(答案不唯一).

练习册系列答案
相关题目