ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§![]() гые§БШР§КЏЪ§
гые§БШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() ЃЌЧвгы
ЃЌЧвгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
(1)жБНгаДГіЕу![]() ЕФзјБъЮЊ ЃЛЕу
ЕФзјБъЮЊ ЃЛЕу![]() ЕФзјБъЮЊ ЃЛ
ЕФзјБъЮЊ ЃЛ
(2)Й§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯпlЁЮyжсЃЎЖЏЕу
зїжБЯпlЁЮyжсЃЎЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы
ГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЕФЫйЖШЃЌби
ИіЕЅЮЛГЄЕФЫйЖШЃЌби![]() ЕФТЗЯпЯђЕу
ЕФТЗЯпЯђЕу![]() дЫЖЏЃЛЭЌЪБжБЯп
дЫЖЏЃЛЭЌЪБжБЯп![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдЯрЭЌЫйЖШЯђзѓЦНвЦЃЌдкЦНвЦЙ§ГЬжаЃЌжБЯп
ГіЗЂЃЌвдЯрЭЌЫйЖШЯђзѓЦНвЦЃЌдкЦНвЦЙ§ГЬжаЃЌжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛЯпЖЮ
ЃЌНЛЯпЖЮ![]() ЛђЯпЖЮ
ЛђЯпЖЮ![]() гкЕу
гкЕу![]() ЃЎЕБЕу
ЃЎЕБЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЪБЃЌЕу
ЪБЃЌЕу![]() КЭжБЯп
КЭжБЯп![]() ЖМЭЃжЙдЫЖЏЃЎдкдЫЖЏЙ§ГЬжаЃЌЩшЖЏЕу
ЖМЭЃжЙдЫЖЏЃЎдкдЫЖЏЙ§ГЬжаЃЌЩшЖЏЕу![]() дЫЖЏЕФЪБМфЮЊ
дЫЖЏЕФЪБМфЮЊ![]() УыЃЎ
УыЃЎ
![]() ЕБ
ЕБ![]() ЮЊКЮжЕЪБЃЌвд
ЮЊКЮжЕЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЮЊ
ЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЮЊ![]() ЃЛ
ЃЛ
![]() ЪЧЗёДцдквд
ЪЧЗёДцдквд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮ?ШєДцдкЃЌжБНгаДГі
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮ?ШєДцдкЃЌжБНгаДГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)![]() ЃЛ(2)ЂйЕБ
ЃЛ(2)ЂйЕБ![]() ЪБЃЌвд
ЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЮЊ
ЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЮЊ![]() ЃЛЂк
ЃЛЂк![]() Лђ
Лђ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЪБЃЌ
ЪБЃЌ![]() ЪЧЕШбќШ§НЧаЮ.
ЪЧЕШбќШ§НЧаЮ.
ЁОНтЮіЁП
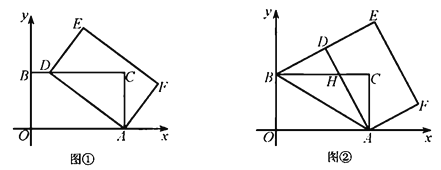
ЃЈ1ЃЉИљОнЭМЯѓгызјБъжсНЛЕуЧѓЗЈжБНгЕУГіМДПЩЃЌдйРћгУжБЯпНЛЕузјБъЧѓЗЈНЋСНжБЯпНтЮіЪНСЊСЂМДПЩЕУГіНЛЕузјБъЃЛ
ЃЈ2ЃЉЂйРћгУSЬнаЮACOBЉSЁїACPЉSЁїPORЉSЁїARBЃН8ЃЌБэЪОГіИїВПЗжЕФБпГЄЃЌећРэГівЛдЊЖўДЮЗНГЬЃЌЧѓГіМДПЩЃЛ
ЂкИљОнвЛДЮКЏЪ§гызјБъжсЕФНЛЕуЕУГіЃЌЁЯOBNЃНЁЯONBЃН45ЁуЃЌНјЖјРћгУЙДЙЩЖЈРэвдМАЕШбќШ§НЧаЮЕФаджЪКЭжБНЧШ§НЧаЮЕФХаЖЈЧѓГіМДПЩЃЎ
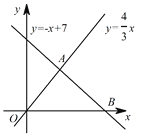
ЃЈ1ЃЉЁпвЛДЮКЏЪ§yЃНЉx+7гые§БШР§КЏЪ§y![]() xЕФЭМЯѓНЛгкЕуAЃЌЧвгыxжсНЛгкЕуBЃЌ
xЕФЭМЯѓНЛгкЕуAЃЌЧвгыxжсНЛгкЕуBЃЌ
Ёр ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрAЕузјБъЮЊЃКЃЈ3ЃЌ4ЃЉЃЛ
ЁпyЃНЉx+7ЃН0ЃЌНтЕУЃКxЃН7ЃЌ
ЁрBЕузјБъЮЊЃКЃЈ7ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉЂйЕБPдкOCЩЯдЫЖЏЪБЃЌ0ЁмtЃМ4ЪБЃЌPOЃНtЃЌPCЃН4ЉtЃЌBRЃНtЃЌORЃН7ЉtЃЎ
ЁпЕБвдAЁЂPЁЂRЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЮЊ8ЃЌ
ЁрSЬнаЮACOBЉSЁїACPЉSЁїPORЉSЁїARBЃН8ЃЌ
Ёр![]() ЃЈAC+BOЃЉЁСCO
ЃЈAC+BOЃЉЁСCO![]() ACЁСCP
ACЁСCP![]() POЁСRO
POЁСRO![]() AMЁСBRЃН8ЃЌ
AMЁСBRЃН8ЃЌ
ЁрЃЈAC+BOЃЉЁСCOЉACЁСCPЉPOЁСROЉAMЁСBRЃН16ЃЌ
ЁрЃЈ3+7ЃЉЁС4Љ3ЁСЃЈ4ЉtЃЉЉtЁСЃЈ7ЉtЃЉЉ4tЃН16ЃЌ
Ёрt2Љ8t+12ЃН0ЃЌНтЕУЃКt1ЃН2ЃЌt2ЃН6ЃЈЩсШЅЃЉЃЛ
ЕБtЃН4ЪБЃЌAЃЌPЃЌRШ§ЕуПЩвдЙЙГЩШ§НЧаЮЃЌДЫЪБУцЛ§ЪЧ6ЃЌВЛКЯЬтвтЃЛ
ЕБ4ЃМtЃМ7ЪБЃЌSЁїAPR![]() APЁСOCЃН2ЃЈ7ЉtЃЉЃН8ЃЌНтЕУЃКtЃН3ЃЌВЛЗћКЯ4ЃМtЃМ7ЃЛ
APЁСOCЃН2ЃЈ7ЉtЃЉЃН8ЃЌНтЕУЃКtЃН3ЃЌВЛЗћКЯ4ЃМtЃМ7ЃЛ
злЩЯЫљЪіЃКЕБtЃН2ЪБЃЌвдAЁЂPЁЂRЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§ЮЊ8ЃЛ
ЂкДцдкЃЎбгГЄCAЕНжБЯпlНЛгквЛЕуDЃЌЕБlгыABЯрНЛгкQЃЎ
ЁпвЛДЮКЏЪ§yЃНЉx+7гыxжсНЛгкЃЈ7ЃЌ0ЃЉЕуЃЌгыyжсНЛгкЃЈ0ЃЌ7ЃЉЕуЃЌ
ЁрNOЃНOBЃЌ
ЁрЁЯOBNЃНЁЯONBЃН45ЁуЃЎ
ЁпжБЯпlЁЮyжсЃЌ
ЁрRQЃНRBЃЌCDЁЭLЃЌ
ЕБ0ЁмtЃМ4ЪБЃЌШчЭМ1ЃЌRBЃНOPЃНQRЃНtЃЌDQЃНADЃНЃЈ4ЉtЃЉЃЌACЃН3ЃЌPCЃН4ЉtЃЎ
ЁпвдAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌдђAPЃНAQЃЌ
ЁрAC2+PC2ЃНAP2ЃНAQ2ЃНЃЈ![]() ADЃЉ2ЃЌ
ADЃЉ2ЃЌ
Ёр9+ЃЈ4ЉtЃЉ2ЃН2ЃЈ4ЉtЃЉ2ЃЌНтЕУЃКt1ЃН1ЃЌt2ЃН7ЃЈЩсШЅЃЉЃЌ
ЕБAPЃНPQЪБ 32+ЃЈ4ЉtЃЉ2ЃНЃЈ7ЉtЃЉ2ЃЌНтЕУЃКtЃН4 ЃЈЩсШЅЃЉЃЎ
ЕБPQЃНAQЪБЃЌ2ЃЈ4ЉtЃЉ2ЃНЃЈ7ЉtЃЉ2ЃЌНтЕУЃКt1ЃН1+3![]() ЃЈЩсШЅЃЉЃЌt2ЃН1Љ3
ЃЈЩсШЅЃЉЃЌt2ЃН1Љ3![]() ЃЈЩсШЅЃЉЃЌЕБtЃН4ЪБЃЌЮоЗЈЙЙГЩШ§НЧаЮЃЛ
ЃЈЩсШЅЃЉЃЌЕБtЃН4ЪБЃЌЮоЗЈЙЙГЩШ§НЧаЮЃЛ
ЕБ4ЃМtЃМ7ЪБЃЌШчЭМЃЈБИгУЭМЃЉЃЌЙ§AзїADЁЭOBгкDЃЌдђADЃНBDЃН4ЃЌЩшжБЯпlНЛACгкEЃЌдђQEЁЭACЃЌAEЃНRDЃНtЉ4ЃЌAPЃН7ЉtЃЌгЩcosЁЯOAC![]() ЃЌЕУЃКAQ
ЃЌЕУЃКAQ![]() ЃЈtЉ4ЃЉЃЌШєAQЃНAPЃЌдђ
ЃЈtЉ4ЃЉЃЌШєAQЃНAPЃЌдђ![]() ЃЈtЉ4ЃЉЃН7ЉtЃЌНтЕУЃКt
ЃЈtЉ4ЃЉЃН7ЉtЃЌНтЕУЃКt![]() ЃЛ
ЃЛ
ЕБAQЃНPQЪБЃЌAEЃНPEЃЌМДAE![]() APЃЌЕУЃКtЉ4
APЃЌЕУЃКtЉ4![]() ЃЈ7ЉtЃЉЃЌНтЕУЃКtЃН5ЃЛ
ЃЈ7ЉtЃЉЃЌНтЕУЃКtЃН5ЃЛ
ЕБAPЃНPQЪБЃЌЙ§PзїPFЁЭAQгкFЃЌAF![]() AQ
AQ![]() ЃЈtЉ4ЃЉЃЎ
ЃЈtЉ4ЃЉЃЎ
дкRtЁїAPFжаЃЌгЩcosЁЯPAF![]() ЃЌЕУЃКAF
ЃЌЕУЃКAF![]() APЃЌМД
APЃЌМД![]() ЃЈtЉ4ЃЉ
ЃЈtЉ4ЃЉ![]() ЃЈ7ЉtЃЉЃЌНтЕУЃКt
ЃЈ7ЉtЃЉЃЌНтЕУЃКt![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКЕБtЃН1ЁЂ5ЁЂ![]() ЁЂ
ЁЂ![]() УыЪБЃЌДцдквдAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЎ
УыЪБЃЌДцдквдAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЎ

 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ