题目内容
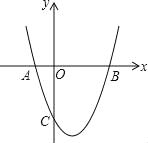
【题目】如图,抛物线y=![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
【答案】(1) y=![]() ﹣2x﹣3;(2)①证明详见解析;②△AEF是等腰直角三角形,理由详见解析.
﹣2x﹣3;(2)①证明详见解析;②△AEF是等腰直角三角形,理由详见解析.
【解析】
试题分析:(1)将A、B、C三点坐标代入抛物线方程,即可求得a、b、c的值;
(2)①由B、C、D三点的坐标即可得出∠CBO=∠OBD=45°,从而得出∠EBF=90°,即可得出EF为圆的直径;
②利用同圆内,同弧所对的圆周角相等,可以找到∠AEF=∠AFE=45°,从而得出△AEF是等腰直角三角形.
试题解析:(1)∵抛物线y=![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3),
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3),
∴ ,解得
,解得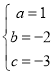 ,
,
∴抛物线的解析式为y=![]() ﹣2x﹣3;
﹣2x﹣3;
(2)按照题意画出图形,如下图,
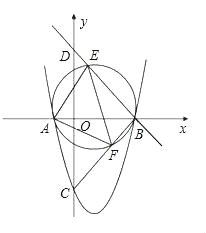
①∵B点坐标(3,0)、C点坐标(0,﹣3),
∴OB=OC=3,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
又∵D是y轴正半轴上的点,OD=3,
∴△BOD为等腰直接三角形,
∴∠OBD=45°,
∠CBD=∠CBO+∠OBD=45°+45°=90°,
即∠FBE=90°,
∴EF是圆的直径.
②∵∠CBO=∠OBD=45°,∠AFE=∠OBD,∠AEF=∠CBO(在同圆中,同弧所对的圆周角相等),
∴∠AEF=∠AFE=45°,
∴∠FAE=90°,AE=AF,
∴△AEF是等腰直角三角形.

练习册系列答案
相关题目