题目内容
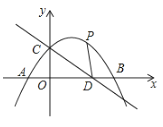
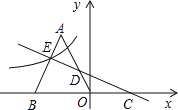
【题目】如图,![]() 为等边三角形,点
为等边三角形,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上,当
的图像上,当![]() 和
和![]() 的面积相等时,
的面积相等时,![]() 的值是__________.
的值是__________.
【答案】![]()
【解析】
根据![]() 和
和![]() 的面积可知S△ABO=S△BEC,由等边三角形性质可求S△ABO,即可求出△BEC的EF长,再根据∠ABC=60°,求出点E的坐标,从而求出k值,得出解析式..
的面积可知S△ABO=S△BEC,由等边三角形性质可求S△ABO,即可求出△BEC的EF长,再根据∠ABC=60°,求出点E的坐标,从而求出k值,得出解析式..
解:过A点作AG⊥BO于G,过E点作EF⊥BO于F,

∵点B的坐标为(-2,0),△AOB为等边三角形,
∵AO=OC=2,∠AOB=60°,
∴AG=OAsin∠ABO=![]() =
=![]() ,BF=
,BF=![]() =
=![]()
∵S△ADE=S△DCO,
∴S△ABO=S△BEC,
∴![]() ×BOAG=
×BOAG=![]() BCEF,即
BCEF,即![]()
∴EF=![]() ,
,
∴BF=![]() =
=![]() ,FO=
,FO=![]() ,
,
把E点(-![]() ,
,![]() )
)
![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目