题目内容
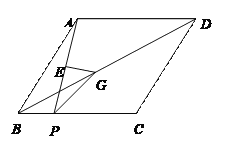
【题目】如图1,![]() 和
和![]() 均为等腰三角形,且
均为等腰三角形,且![]() ,连接
,连接![]() ,
,![]() ,两条线段所在的直线交于点
,两条线段所在的直线交于点![]() .
.
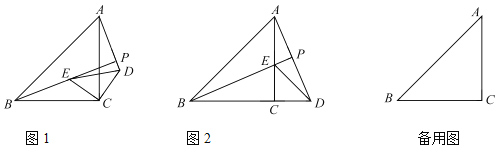
(1)线段![]() 与
与![]() 有何数量关系和位置关系,请说明理由.
有何数量关系和位置关系,请说明理由.
(2)若已知![]() ,
,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,
①如图2,当点![]() 恰好落在
恰好落在![]() 的延长线上时,求
的延长线上时,求![]() 的长;
的长;
②在旋转一周的过程中,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最值.
的最值.
【答案】(1)![]() ,
,![]() 与
与![]() 互相垂直(2)①
互相垂直(2)①![]() ②47、72
②47、72
【解析】
(1)证明![]() ,根据全等三角形的性质进行求解即可.
,根据全等三角形的性质进行求解即可.
(2)①求出![]() ,根据勾股定理求出
,根据勾股定理求出![]() ,证明
,证明![]() ,根据相似三角形的性质即可求出.
,根据相似三角形的性质即可求出.
②由![]() 可知点
可知点![]() 在以
在以![]() 为直径的圆的一段弧上,且当
为直径的圆的一段弧上,且当![]() 与以
与以![]() 为半径
为半径![]() 相切时,点
相切时,点![]() 在其运动路径所在弧的两个端点处,
在其运动路径所在弧的两个端点处,![]() 到
到![]() 的距离最小,此时
的距离最小,此时![]() 的面积
的面积![]() 最小, 当点
最小, 当点![]() 与点
与点![]() 重合时,
重合时,![]() 到
到![]() 的距离最大,此时
的距离最大,此时![]() 的面积
的面积![]() 最大,求解即可.
最大,求解即可.
(1)![]() ,
,![]() 与
与![]() 互相垂直;
互相垂直;
证明:∵等腰![]() ,等腰
,等腰![]() ,
,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]() ,
,![]() ,
,
∵![]()
∴![]() ,即
,即![]() 与
与![]() 互相垂直
互相垂直
(2)①∵![]() ,
,![]()
∴![]() ,
,
![]() 中,
中, ![]() ,
,
由(1)同理可知![]() ,
,![]()
∴![]()
∴![]() ,即
,即![]() ,解得
,解得![]()
②由![]() 可知点
可知点![]() 在以
在以![]() 为直径的圆的一段弧上,且当
为直径的圆的一段弧上,且当![]() 与以
与以![]() 为半径
为半径![]() 相切时,点
相切时,点![]() 在其运动路径所在弧的两个端点处,
在其运动路径所在弧的两个端点处,![]() 到
到![]() 的距离最小,此时
的距离最小,此时![]() 的面积
的面积![]() 最小,如图1、2,易知四边形
最小,如图1、2,易知四边形![]() 是边长为5的正方形.
是边长为5的正方形.
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,
,
当点![]() 与点
与点![]() 重合时,
重合时,![]() 到
到![]() 的距离最大,此时
的距离最大,此时![]() 的面积
的面积![]() 最大,如图3
最大,如图3

![]() .
.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目