题目内容
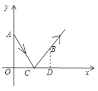
【题目】受疫情的影响，很多农产品滞销，各大电商发起了“爱心助农”活动，帮助农户进行农产品销售．已知某种橘子的成本为4元/千克，经过市场调查发现，一天内橘子的销售量y(千克)与销售单价x(元/千克)(4≤x≤10)的函数关系如下图所示：
（1）当4≤x≤8时，求y与x的函数解析式；
（2）当4≤x≤8时，要使一天内获得的利润为1200元，单价应定为多少？
（3）求橘子的单价定为多少时，一天内获得的利润最大，最大利润为多少？
【答案】（1）y=－200x+1800(4≤x≤8)；（2）单价定为6元或7元，利润为1200元；（3）当橘子的单价为6.5元时，获得利润的最大值为1250元．
【解析】
（1）由题意设y=kx＋b(k≠0)，利用待定系数法把点(4，1000)与点(8，200)代入进行求解即可得出y与x的函数解析式；
（2）根据题意一天内获得的利润为1200元建立方程进行求解即可得出单价，注意x的取值范围；
（3）根据题意设利润为w元，由题意建立不等式求解进而得出橘子的单价和最大利润．
解：（1）当4≤x≤8时，由题意设y=kx＋b(k≠0)，
它的图象经过点(4，1000)与点(8，200)，有
，
解得
，
∴当4≤x≤8时，y=－200x+1800.
（2）当4≤x≤8时，由题意(x－4)(－200x＋1800)=1200
解得
，
，
∴当4≤x≤8时，单价定为6元或7元，利润为1200元.
（3）设利润为w元，
当4≤x≤8时，y=－200x＋1800，
w=(x－4)y=(x－4)(－200x＋1800)=
∵－200＜0，4≤x≤8，
当x=
时，w有最大值，此时w=1250；
当8＜x≤10时，y=200，w=(x－4)y=200(x－4)=200x－800．
∵200＞0，
∴w=200x－800随x增大而增大，
又∵8＜x≤10，
∴当x=10时，w最大，此时w=1200．
∵1250＞1200，
∴w的最大值为1250．
答：当橘子的单价为6.5元时，获得利润的最大值为1250元．
