题目内容
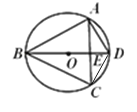
【题目】如图,四边形ABCD内接于直径为3的⊙O,AB=AC,E是弦AC和直径BD的交点,ED=![]() ,则弦AD的长为( )
,则弦AD的长为( )
A.![]() B.2C.
B.2C.![]() D.
D.![]()
【答案】A
【解析】
连接AO并延长交BC于H,得到AH⊥BC,可以证明三角形相似,利用相似三角形的性质求出CD的长,然后利用勾股定理分别求出BC、AB、AD的长.
解:连接AO并延长交BC于H,
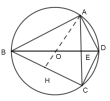
∵ΔABC是⊙O的内接三角形,AB=AC,
∴AH⊥BC,BH=CH,
∵∠BCD=90,
∴AH∥CD,
∴ΔAOE∽ΔCDE,
∴![]() ,
,
∵OA=1.5,DE=![]() =0.6,
=0.6,
∴![]() ,
,
∴CD=1,
∴BC=![]() =
=![]() =
=![]() ,
,
∵BH=CH,OB=OD,
∴OH是ΔBCD的中位线,
∴OH=![]() CD=
CD=![]() ,
,
∴AH=2,
∴AB=![]() =
=![]() =
=![]() ,
,
AD=![]() =
=![]() .
.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目