题目内容
【题目】某校组织学生开展了“2020新冠疫情”相关的手抄报竞赛.对于手抄报的主题,组织者提出了两条指导性建议:
(1)A类“武汉加油”、B类“最美逆行者”、C类“万众一心抗击疫情”、D类“如何预防新型冠状病毒”4个中任选一个;
(2)E类为自拟其它与疫情相关的主题.
评奖之余,为了解学生的选题倾向,发掘出最能引发学生触动的主题素材,组织者随机抽取了部分作品进行了统计,并将统计结果绘制成了如下两幅尚不完整的统计图.
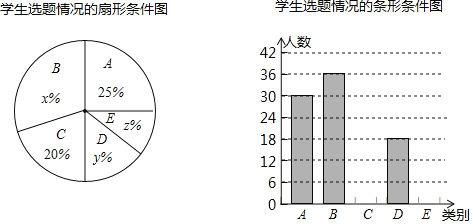
请根据以上信息回答:
(1)本次抽样调查的学生总人数是 ,并补全条形统计图;
(2)扇形统计图中,“C”对应的扇形圆心角的度数是 ,x= ,y﹣z= ;
(3)本次抽样调查中,“学生手抄报选题”最为广泛的是 类.(填字母)
【答案】(1)120;补全条形统计图见解析;(2)72°,30,5;(3)B.
【解析】
(1)利用扇形统计图结合条形统计图,进而得出调查的总人数和C,E两组的人数;
(2)根据(1)中所求总人数,进而结合条形统计图可得答案;
(3)利用(2)中所求得出B类所占比例最多,进而得出答案.
解:(1)调查的学生总人数:30÷25%=120(人),
120×20%=24(人),
120﹣30﹣36﹣24﹣18=12(人),
如图所示:
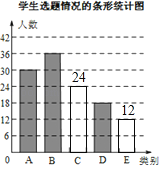
(2)“C”对应的扇形圆心角的度数是:360°×20%=72°,
x%=![]() ×100%=30%,y%=
×100%=30%,y%=![]() ×100%=15%,z%=1﹣30%﹣15%﹣25%﹣20%=10%,
×100%=15%,z%=1﹣30%﹣15%﹣25%﹣20%=10%,
故x=30,y﹣z=10﹣5=5,
故答案为:72°,30,5;
(3)由(2)中所求,可得出:“学生手抄报选题”最为广泛的是B类.
故答案为:B.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数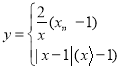 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
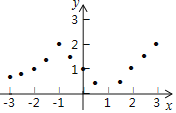
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.