题目内容
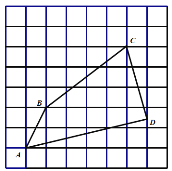
【题目】如图,在每个边长为1的小正方形的网格中,△ABC的顶点A,B,C在格点上,P是BC边上任意一点,以A为中心,取旋转角等于∠BAC,把点P逆时针旋转,点P的对应点为点P',当CP'最短时,画出点P',并说明CP'最短的理由是______.
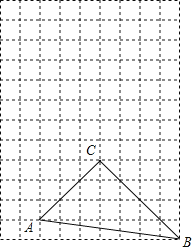
【答案】垂线段最短.
【解析】
连CF,根据已知条件得到A、C、F共线,求得AF=5![]() =AB,根据相似三角形的想知道的∠GFC=∠B,求得∠TCA=∠TAC,得到CP′⊥GF,于是得到结论.
=AB,根据相似三角形的想知道的∠GFC=∠B,求得∠TCA=∠TAC,得到CP′⊥GF,于是得到结论.
解:作图过程如下:
取格点D,E,连接DE交AB于点T;取格点M,N,连接MN交BC延长线于点G:取格点F,连接FG交TC延长线于点P′,则点P′即为所求
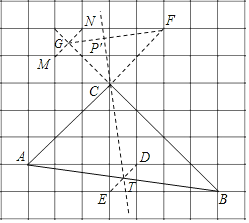
证明:连CF,
∵AC,CF为正方形网格对角线
∴A、C、F共线
∴AF=5![]() =AB,
=AB,
由图形可知:GC=![]() ,CF=2
,CF=2![]() ,
,
∵AC=![]() =3
=3![]() ,BC=4
,BC=4![]() ,
,
∴△ACB∽△GCF,
∴∠GFC=∠B,
∵AF=5![]() =AB,
=AB,
∴当BC边绕点A逆时针旋转∠CAB时,点B与点F重合,点C在射线FG上.
由作图可知T为AB中点,
∴∠TCA=∠TAC,
∴∠F+∠P′CF=∠B+∠TCA=∠B+∠TAC=90°,
∴CP′⊥GF,
此时,CP′最短,
故答案为垂线段最短.

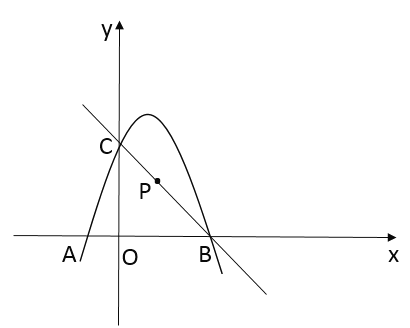
【题目】如图,Rt△ABC中,∠C = 90°, P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q . 已知AC = 3cm,BC = 6cm,设PC的长度为xcm,BQ的长度为ycm .

小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1) 按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x ,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y > 2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?(直接写结果)
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数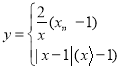 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
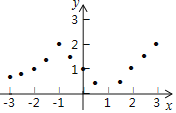
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.