题目内容
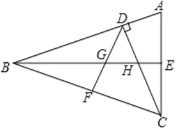
【题目】下面是“作三角形一边中线”的尺规作图过程. 已知:△ABC(如图1),求作:BC边上的中线AD.
作法:如图2,
(i)分别以点B,C为圆心,AC,AB长为半径作弧,两弧相交于P点;
(ii)作直线AP,AP与BC交于D点.
所以线段AD就是所求作的中线.
请回答:该作图的依据是 .
【答案】两组对边分别相等的四边形是平行四边形,平行四边形的对角线互相平分
【解析】解:由作法得BP=AC,CP=AB,则四边形ABPC为平行四边形, 所以BD=CD,即点D为BC的中点,
所以AD为中线.
所以答案是两组对边分别相等的四边形是平行四边形,平行四边形的对角线互相平分.
【考点精析】利用平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目