题目内容
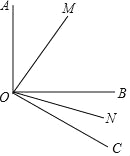
【题目】如图,已知OM平分∠AOB,ON平分∠BOC.
(1)若∠AOB=90°,∠BOC=30°,则∠MON=_____;
(2)若∠AOB=α,∠BOC=β,其它条件不变,则∠MON=______;
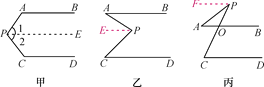
(3)当OC运动到∠AOB内部时,其余条件不变,请你画出图形并猜想∠MON与∠AOB、∠BOC的数量关系式,并说明理由.
【答案】(1)60°;(2)![]() (α+β);(3)∠MON=
(α+β);(3)∠MON=![]() (∠AOB﹣∠BOC).
(∠AOB﹣∠BOC).
【解析】
(1)根据角平分线的定义求得∠MOB,∠BON,再根据角的和差关系即可求解;
(2)根据角平分线的定义求得∠MOB,∠BON,再根据角的和差关系即可求解;
(3)根据角平分线的定义求得∠MOB,∠BON,再根据角的和差关系即可求解.
解:(1)∵∠AOB=90°,∠BOC=30°,OM,ON分别平分∠AOB,∠BOC,
∴∠MOB=![]() ∠AOB=45°,∠BON=
∠AOB=45°,∠BON=![]() ∠BOC=15°,
∠BOC=15°,
∴∠MON=∠MOB+∠BON=60°.
故答案为:60°;
(2)∵∠AOB=α,∠BOC=β,OM,ON分别平分∠AOB,∠BOC,
∴∠MOB=![]() ∠AOB=
∠AOB=![]() α,∠BON=
α,∠BON=![]() ∠BOC=
∠BOC=![]() β,
β,
∴∠MON=∠MOB+∠BON=![]() (α+β).
(α+β).
故答案为:![]() (α+β);
(α+β);
(3)∵OM,ON分别平分∠AOB,∠BOC,
∴∠MOB=![]() ∠AOB,∠CON=
∠AOB,∠CON=![]() ∠BOC,
∠BOC,
∴∠MON=∠MOB﹣∠CON=![]() (∠AOB﹣∠BOC).
(∠AOB﹣∠BOC).

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】如图所示,为厉行节能减排,倡导绿色出行,某公司拟在我市甲、乙两个街道社区投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型.
成本单价 (单位:元) | 投放数量 (单位:辆) | 总价(单位:元) | |
A型 | x | 50 | 50x |
B型 | x+10 | 50 |
|
成本合计(单位:元) | 7500 | ||
问题1:看表填空
如图2所示,本次试点投放的A、B型“小黄车”共有 辆;用含有x的式子表示出B型自行车的成本总价为 ;
问题2:自行车单价
试求A、B两型自行车的单价各是多少?
问题3:投放数量
现在该公司采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.

【题目】为了迎接“六一”国际儿童节,某童装品牌专卖店准备购进甲、乙两种童装,这两种童装的进价和售价如下表:
价格 | 甲 | 乙 |
进价(元/件) | m | m+20 |
售价(元/件) | 150 | 160 |
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种童装共200件的总利润(利润=售价﹣进价)不少于8980元,且甲种童装少于100件,问该专卖店有哪几种进货方案?