��Ŀ����
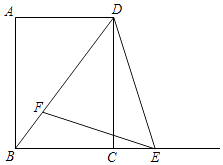
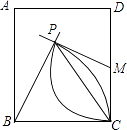
����Ŀ����ͼ����ֱ��������ABC�У���ACB=90�㣬AB=10��sinB= ![]() ����O��AB���е㣬��DOE=��A������DOE�Ե�OΪ��ת������תʱ��OD��AC���ӳ����ڵ�D������CB�ڵ�M��OE���߶�BM�ڵ�N��
����O��AB���е㣬��DOE=��A������DOE�Ե�OΪ��ת������תʱ��OD��AC���ӳ����ڵ�D������CB�ڵ�M��OE���߶�BM�ڵ�N��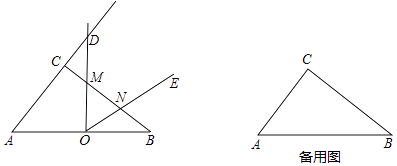
��1����CM=2ʱ�����߶�CD�ij���
��2����CM=x��BN=y������y��x֮��ĺ�������ʽ����д��������
��3�������OMN����OMΪ���ĵ��������Σ���ֱ��д���߶�CM�ij���
���𰸡�
��1��
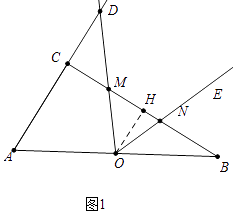
�⣺��ͼ1�У���OH��BC��H��
��Rt��ABC����AB=10��sinB= ![]() ��
��
��AC=6��BC=8��
��AO=OB��OH��AC��
��CH=HB=4��OH=3��
��CM=2��
��CM=HM=2��
�ڡ�DCM�͡�OHM�У�
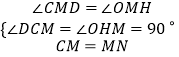 ��
��
���DCM�ա�OHM��
��CD=OH=3��
��2��
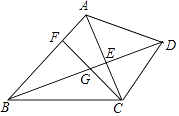
�⣺�⣺��ͼ2�У���NG��OB��G��
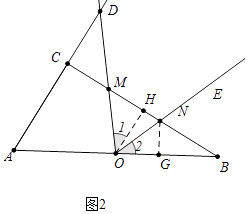
�ߡ�HOB=��A=��MON��
���1=��2��
��Rt��BNG��BN=y��sibB= ![]() ��
��
��GN= ![]() y��BG=
y��BG= ![]() y��
y��
��tan��1=tan��2��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��y= ![]() ����0��x��4��
����0��x��4��
��3��
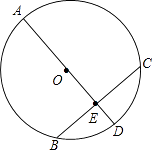
����ͼ3�У���OM=ONʱ��OH��ֱƽ��MN��
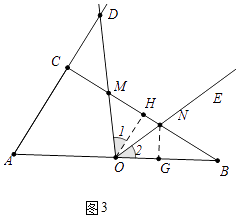
��BN=CM=x��
�ߡ�OMH�ա�ONG��
��NG=HM=4��x��
��sinB= ![]() ��
��
�� ![]() =
= ![]() ��
��
��CM=x= ![]() ��
��
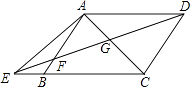
����ͼ4�У���OM=MNʱ������CO��
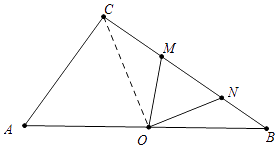
��OA=OB��OM=MN��
��CO=OA=OB��
���MON=��MNO=��A=��OCA��
���MON�ס�OAC��
���AOC=��OMN��
���BOC=��CMO���ߡ�B=��B��
���CMO�ס�COB��
�� ![]() =
= ![]() ��
��
��8x=52��
��x= ![]() ��
��
������������OMN����OMΪ���ĵ���������ʱ���߶�CM�ij�Ϊ ![]() ��
�� ![]()
����������1����ͼ1�У���OH��BC��H��ֻҪ֤����DCM�ա�OHM�����ɵó�CD=OH=3����2����ͼ2�У���NG��OB��G������֤����1=��2������tan��1=tan��2���ɵ� ![]() =
= ![]() ���ɴ˼��ɽ�����⣮��3���������������ۼ��ɢ���ͼ3�У���OM=ONʱ��OH��ֱƽ��MN������ͼ4�У���OM=MNʱ���ֱ���⼴�ɣ�
���ɴ˼��ɽ�����⣮��3���������������ۼ��ɢ���ͼ3�У���OM=ONʱ��OH��ֱƽ��MN������ͼ4�У���OM=MNʱ���ֱ���⼴�ɣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�