ЬтФПФкШн
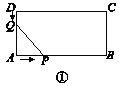
ЁОЬтФПЁПШчЭМЫљЪОЃЌФГЙЄГЬЖгзМБИдкЩНЦТЃЈЩНЦТЪгЮЊжБЯпlЃЉЩЯаовЛЬѕТЗЃЌашвЊВтСПЩНЦТЕФЦТЖШЃЌМДtanІСЕФжЕЃЎВтСПдБдкЩНЦТPДІЃЈВЛМЦДЫШЫЩэИпЃЉЙлВьЖдУцЩНЖЅЩЯЕФвЛзљЬњЫўЃЌВтЕУЫўМтCЕФбіНЧЮЊ31ЁуЃЌЫўЕзBЕФбіНЧЮЊ26.6ЁуЃЎвбжЊЫўИпBC=40УзЃЌЫўЫљдкЕФЩНИпOB=240УзЃЌOA=300УзЃЌЭМжаЕФЕуOЁЂBЁЂCЁЂAЁЂPдкЭЌвЛЦНУцФкЃЎЧѓЃК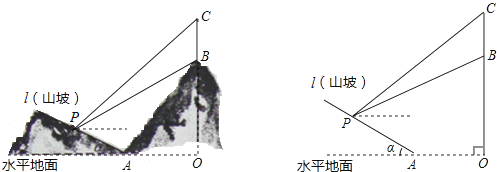
ЃЈ1ЃЉPЕНOCЕФОрРыЃЎ
ЃЈ2ЃЉЩНЦТЕФЦТЖШtanІСЃЎ
ЃЈВЮПМЪ§Онsin26.6ЁуЁж0.45ЃЌtan26.6ЁуЁж0.50ЃЛsin31ЁуЁж0.52ЃЌtan31ЁуЁж0.60ЃЉ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКШчЭМЃЌЙ§ЕуPзїPDЁЭOCгкDЃЌPEЁЭOAгкEЃЌдђЫФБпаЮODPEЮЊОиаЮЃЎ
дкRtЁїPBDжаЃЌЁпЁЯBDP=90ЁуЃЌЁЯBPD=26.6ЁуЃЌ
ЁрBD=PDtanЁЯBPD=PDtan26.6ЁуЃЛ
дкRtЁїCPDжаЃЌЁпЁЯCDP=90ЁуЃЌЁЯCPD=31ЁуЃЌ
ЁрCD=PDtanЁЯCPD=PDtan31ЁуЃЛ
ЁпCDЉBD=BCЃЌ
ЁрPDtan31ЁуЉPDtan26.6Ёу=40ЃЌ
Ёр0.60PDЉ0.50PD=40ЃЌ
НтЕУPD=400ЃЈУзЃЉЃЌ
ЁрPЕНOCЕФОрРыЮЊ400Уз
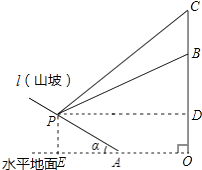
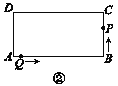
ЃЈ2ЃЉ
НтЃКдкRtЁїPBDжаЃЌBD=PDtan26.6ЁуЁж400ЁС0.50=200ЃЈУзЃЉЃЌ
ЁпOB=240УзЃЌ
ЁрPE=OD=OBЉBD=40УзЃЌ
ЁпOE=PD=400УзЃЌ
ЁрAE=OEЉOA=400Љ300=100ЃЈУзЃЉЃЌ
ЁрtanІС= ![]() =
= ![]() =0.4ЃЌ
=0.4ЃЌ
ЁрЦТЖШЮЊ0.4
ЁОНтЮіЁПЃЈ1ЃЉЙ§ЕуPзїPDЁЭOCгкDЃЌPEЁЭOAгкEЃЌдђЫФБпаЮODPEЮЊОиаЮЃЌЯШНтRtЁїPBDЃЌЕУГіBD=PDtan26.6ЁуЃЛНтRtЁїCPDЃЌЕУГіCD=PDtan31ЁуЃЛдйИљОнCDЉBD=BCЃЌСаГіЗНГЬЃЌЧѓГіPD=400МДПЩЧѓЕУЕуPЕНOCЕФОрРыЃЛЃЈ2ЃЉРћгУЧѓЕУЕФЯпЖЮPDЕФГЄЧѓГіPE=40ЃЌAE=100ЃЌШЛКѓдкЁїAPEжаРћгУШ§НЧКЏЪ§ЕФЖЈвхМДПЩЧѓНтЃЎ

ЁОЬтФПЁПШчЭМЪЧЩњЛюжаГЃМћЕФдТРњЕФЪОвтЭМЃЌЧыНсКЯЭМЪОЛиД№ЯТСаЮЪЬтЃЎ
вЛ | Жў | Ш§ | ЫФ | Юх | Сљ | Ше |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)ШчЭМЪЧСэвЛИідТЕФдТРњЃЌaБэЪОИУдТжаФГвЛЬьЃЌbЃЌcЃЌdЪЧИУдТжаЦфЫћ3ЬьЃЌbЃЌcЃЌdЗжБ№гыaЕФЙиЯЕЃКbЃН________ЃЛcЃН________ЃЛdЃН________(гУКЌaЕФДњЪ§ЪНЬюПе)ЃЎ
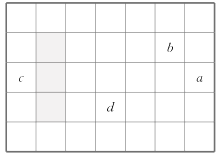
(2)гУвЛИіГЄЗНаЮПђШІГідТРњжаЕФШ§ИіЪ§(Шч ЭМжаЕФвѕгА)ЃЌШєетШ§ИіЪ§жЎКЭЕШгк51ЃЌдђетШ§ИіЪ§ЗжБ№ЪЧЖрЩйЃП
(3)етбљШІГіЕФШ§ИіЪ§ЕФКЭПЩФмЪЧ64Т№ЃПЮЊЪВУДЃП