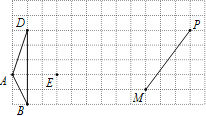题目内容
【题目】在平面直角坐标系中,已知长方形![]() ,点
,点![]() ,
,![]() .
.
(1)如图,有一动点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,若
上,若![]() ,求
,求![]() 的度数;
的度数;
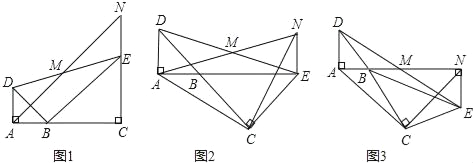
(2)若把长方形![]() 向上平移,得到长方形
向上平移,得到长方形![]() .
.
①在运动过程中,求![]() 的面积与
的面积与![]() 的面积之间的数量关系;
的面积之间的数量关系;
②若![]() ,求
,求![]() 的面积与
的面积与![]() 的面积之比.
的面积之比.
【答案】(1)55°或35°;(2)①![]() ;②
;②![]() .
.
【解析】
(1)分两种情况:①在Rt△FEC中,求出∠FEC=90°-10°=80°,然后根据点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,得出∠POE=45°,对顶角相等,即可得出∠CPO=180°-80°-45°=55°;②由已知条件,得出∠CEO=45°,又根据∠CEO=∠CPE+∠PCB,得出∠CPO;
上,得出∠POE=45°,对顶角相等,即可得出∠CPO=180°-80°-45°=55°;②由已知条件,得出∠CEO=45°,又根据∠CEO=∠CPE+∠PCB,得出∠CPO;
(2)①首先设长方形![]() 向上平移
向上平移![]() 个单位长,得到长方形
个单位长,得到长方形![]() ,然后列出
,然后列出![]() 和
和![]() 的面积,即可得出两者的数量关系;
的面积,即可得出两者的数量关系;
②首先根据已知条件判定四边形![]() 是平行四边形,经过等量转化,即可得出
是平行四边形,经过等量转化,即可得出![]() 和
和![]() 的面积,进而得出其面积之比.
的面积,进而得出其面积之比.
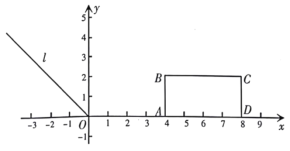
(1)分两种情况:
①令PC交x轴于点E,延长CB至x轴,交于点F,如图所示:
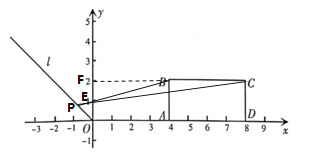
由已知得,![]() ,∠CFE=90°
,∠CFE=90°
∴∠FEC=90°-10°=80°,
又∵点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,
上,
∴∠POE=45°
又∵∠FEC=∠PEO=80°
∴∠CPO=180°-80°-45°=55°
②延长CB,交直线l于点E,
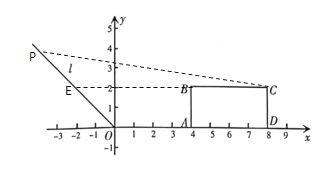
由已知得,![]() ,
,
∵点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,
上,
∴∠CEO=45°
∴∠CEO=∠CPE+∠PCB
∴∠CPO=45°-10°=35°.
故答案为55°或35°.
(2)如图,
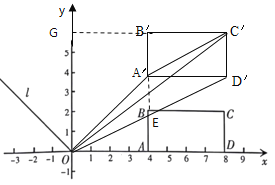
①设长方形![]() 向上平移
向上平移![]() 个单位长,得到长方形
个单位长,得到长方形![]()
![]()
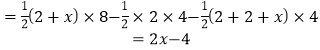
![]()
∴![]()
②∵长方形![]() ,
,
∴![]()
∵![]() ,
,
令![]() 交
交![]() 于E,
于E,
则四边形![]() 是平行四边形,
是平行四边形,
∴![]()
∴![]()
又∵![]()
由①得知,![]()
∴![]()
![]()
∴![]() .
.

练习册系列答案
相关题目