Question

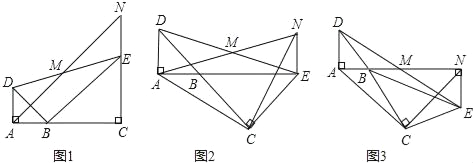
【题目】如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．

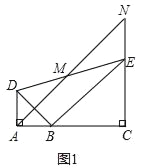
（1）当A，B，C三点在同一直线上时（如图1），直接写出线段AD与NE的数量关系为　 　．

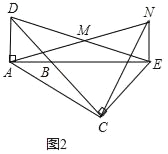
（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），判断△ACN是什么特殊三角形并说明理由．

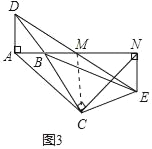
（3）将图1中△BCE绕点B旋转到图3位置，此时A，B，M三点在同一直线上．若AC=3，AD=1，则四边形ACEN的面积为　 　．

Answer 1

【答案】（1）AD=AE；（2）△ACN为等腰直角三角形，理由见解析；（3） .

【解析】试题分析：（1）证明△ADM和△NEM全等，可得AD=NE．（2）△BAD和△BCE均为等腰直角三角形，证明△ABC和△NEC中，可得∠ABC=∠NEC，△ACN为等腰直角三角形．（3）连接CM,先证明△ADM≌△NEM，△ABC≌△NEC，所以 △ACN为等腰直角三角形，

由（1）可知，△AMD≌△NME，利用S四边形ACNE=S△AMC+S直角梯形MNEC.

试题解析：

解：（1）结论：AD=NE,

理由：如图1，

∵EN∥AD，

∴∠MAD=∠MNE，∠ADM=∠NEM,

∵点M为DE的中点，

∴DM=EM,

在△ADM和△NEM中，

,

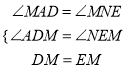∴△ADM≌△NEM,

∴AD=NE．

（2）结论：△ACN为等腰直角三角形．

理由，如图2，

∵△BAD和△BCE均为等腰直角三角形，

∴AB=AD，CB=CE，∠CBE=∠CEB=45°,

∵AD∥NE，

∴∠DAE+∠NEA=180°,

∵∠DAE=90°，

∴∠NEA=90°．

∴∠NEC=135°,

∵A，B，E三点在同一直线上，

∴∠ABC=180°﹣∠CBE=135°,

∴∠ABC=∠NEC,

∵△ADM≌△NEM（已证），

∴AD=NE,

∵AD=AB，

∴AB=NE,

在△ABC和△NEC中，

,

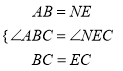∴△ABC≌△NEC,

∴AC=NC，∠ACB=∠NCE,

∴∠ACN=∠BCE=90°,

∴△ACN为等腰直角三角形．

（3）如图3中，连接CM．

∵AD∥NE，M为中点，

∴易得△ADM≌△NEM，

∴AD=NE．

∵AD=AB，

∴AB=NE，

∵AD∥NE，

∴AF⊥NE，

在四边形BCEF中，

∵∠BCE=∠BFE=90°，

∴∠FBC+∠FEC=360°﹣180°=180°

∵∠FBC+∠ABC=180°，

∴∠ABC=∠FEC，

在△ABC和△NEC中，

,

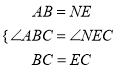∴△ABC≌△NEC，

∴AC=NC，∠ACB=∠NCE，

∴∠ACN=∠BCE=90°，

∴△ACN为等腰直角三角形，

由（1）可知，△AMD≌△NME，

∴AM=MN，AD=NE=1，

∴CM⊥AN，AM=CM=MN，

∵AC=3，

∴AM=CM=MN=3，

∴S四边形ACNE=S△AMC+S直角梯形MNEC=×3×3+×（3+1）×3=．

故答案为．