题目内容
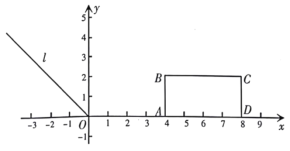
【题目】如图，在平面直角坐标系中有Rt△ABC，∠A＝90°，AB＝AC，A（－2，0）、B（0， d）、C（－3，2）.
（1）求d的值；
（2）将△ABC沿
轴的正方向平移a个单位，在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式；
（3）在（2）的条件下，直线
交y轴于点G，作
⊥
轴于
． 
是线段
上的一点，若△
和△
面积相等，求点
坐标．
【答案】（1）1；（2）
， 
；（3）
【解析】试题分析：（1）作CN⊥x轴于点N，证明Rt△CNA和Rt△AOB，据此即可求出AN=OB=1，进而得解；
（2）分别用含有a的代数式表示出点B′，C′的坐标，并用待定系数法求反比例函数解析式，即可得解；
（3）设出点P的坐标，根据面积相等得到方程，据此即可得解．
试题解析：解：（1）作CN⊥x轴于点N．
在Rt△CNA和Rt△AOB中，∵NC=OA，AC=AB，∴Rt△CNA≌Rt△AOB（HL），则BO=AN=3﹣2=1，∴d=1；
（2）设反比例函数为
，点C′和B′在该比例函数图象上，设C′（a，2），则B′（a+3，1），把点C′和B′的坐标分别代入
，得k=2a；k=a+3，∴2a=a+3，a=3，则k=6，反比例函数解析式为
．得点C′（3，2）；B′（6，1）；
设直线C′B′的解析式为y=ax+b，把C′、B′两点坐标代入得： 
，解得：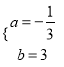 
；
∴直线C′B′的解析式为：y=
；
（3）连结BB′．∵B（0，1），B′（6，1），∴BB′∥x轴，设P（m， 
），作PQ⊥C′M，PH⊥BB′，∴S△PC’M=
×PQ×C′M=
×（m﹣3）×2=m﹣3
S△PBB’=
×PH×BB′=
×（
）×6=﹣m+6
∴m﹣3=﹣m+6
∴m=
∴P（
， 
）．
【题目】利民商场经营某种品牌的T恤，购进时的单价是300元，根据市场调查：在一段时间内，销售单价是400元时，销售量是60件，销售单价每涨10元，销售量就减少1件．设这种T恤的销售单价为x元（x＞400）时，销售量为y件、销售利润为W元．
（1）请分别用含x的代数式表示y和W（把结果填入下表）：
销售单价（元） | x |
销售量y（件） | |
销售利润W（元） |
（2）该商场计划实现销售利润10000元，并尽可能增加销售量，那么x的值应当是多少？
