题目内容
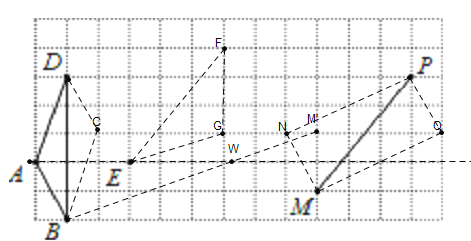
【题目】如图,在13×7的网格中,每个小正方形边长都是1,其顶点叫做格点,如图A、B、D、E、M、P均为格点.
(1)请在网格中画□ABCD,要求C点在格点上.
(2)在(1)中□ABCD右侧画格点△EFG,并使EF=5,FG=3,EG=![]() .
.
(3)以MP为对角线画矩形MNPQ(M、N、P、Q按逆时针方向排列),使矩形MNPQ的面积为10.
(4)在直线AE上有一点W,使WB+WM的值最小,则这个最小值为 .
【答案】(1)见解析;(2)见解析;(3)见解析;(4)![]() .
.
【解析】
(1)根据A,B,D的位置和平行四边形性质找到点C作出即可;
(2)依据EF=5,FG=3,EG=![]() ,确定F,G的位置,作图即可;
,确定F,G的位置,作图即可;
(3)根据MP为对角线及矩形MNPQ的面积为10,从而确定N,Q的位置,作图即可;
(4)过点M作关于直线AE的对称点![]() ,连接
,连接![]() 与AE直线交于点W,则WB+WM的最小值及即
与AE直线交于点W,则WB+WM的最小值及即![]() 的长度,求出即可.
的长度,求出即可.
(1)根据A,B,D的位置和平行四边形两组对边分别平行,从而确定C点位置,作出![]() ,如图所示;
,如图所示;
(2)使EF=5,FG=3,EG=![]() ,则
,则![]() ,
,![]() ,
,
从而确定F,G的位置,△EFG如图所示;
(3)![]() ,
,
以MP为对角线,且使矩形MNPQ的面积为10,
从而确定N,Q的位置,
矩形MNPQ如图所示;
(4)过点M作关于直线AE的对称点![]() ,连接
,连接![]() 与AE直线交于点W,
与AE直线交于点W,
则WB+WM的最小值即![]() 的长度,
的长度,
∴![]() ,
,
则WB+WM的最小值为![]() .
.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.