题目内容
(1)已知A=
,B=
,C=
.将它们组合成(A-B)÷C或A-B÷C的形式,请你从中任选一种进行计算,先化简,再求值,其中x=3.
(2)超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为100米的点P处.这时,一辆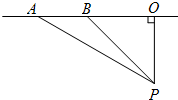 出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.
出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.
①求A、B之间的路程;
②请判断此出租车是否超过了城南大道每小时60千米的限制速度?(参考数据:
≈1.41,
≈1.73).
| 1 |
| x-2 |
| 2 |
| x2-4 |
| x |
| x+2 |
(2)超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为100米的点P处.这时,一辆
 出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.
出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.①求A、B之间的路程;
②请判断此出租车是否超过了城南大道每小时60千米的限制速度?(参考数据:
| 2 |
| 3 |
分析:(1)把表示A、B、C的分式代入(A-B)÷C,进行分式的混合运算,再把x=3代入化简后的式子即可;
(2)①利用三角函数在两个直角三角形中分别计算出BO、AO的长,即可算出AB的长;
②利用路程÷时间=速度,计算出出租车的速度,再把60千米/时化为16.67米/秒,再进行比较即可.
(2)①利用三角函数在两个直角三角形中分别计算出BO、AO的长,即可算出AB的长;
②利用路程÷时间=速度,计算出出租车的速度,再把60千米/时化为16.67米/秒,再进行比较即可.
解答:解:(1)(A-B)÷C
=(
-
)÷
=
•
=
,
当x=3时,原式=
=1;
(2)①由题意知:PO=100米,∠APO=60°,∠BPO=45°,
在直角三角形BPO中,
∵∠BPO=45°,
∴BO=PO=100米,
在直角三角形APO中,
∵∠APO=60°,
∴AO=PB•tan60°=100
米,
∴AB=AO-BO=(100
-100)≈73(米);
②∵从A处行驶到B处所用的时间为4秒,
∴速度为73÷4=18.25米/秒,
60千米/时≈16.67米/秒,
∵18.25>16.67,
∴此车超过了每小时60千米的限制速度.
=(
| 1 |
| x-2 |
| 2 |
| x2-4 |
| x |
| x+2 |
=
| x+2-2 |
| (x-2)(x+2) |
| x+2 |
| x |
=
| 1 |
| x-2 |
当x=3时,原式=
| 1 |
| 3-2 |
(2)①由题意知:PO=100米,∠APO=60°,∠BPO=45°,
在直角三角形BPO中,
∵∠BPO=45°,
∴BO=PO=100米,
在直角三角形APO中,
∵∠APO=60°,
∴AO=PB•tan60°=100
| 3 |
∴AB=AO-BO=(100
| 3 |
②∵从A处行驶到B处所用的时间为4秒,
∴速度为73÷4=18.25米/秒,
60千米/时≈16.67米/秒,
∵18.25>16.67,
∴此车超过了每小时60千米的限制速度.
点评:此题主要考查了分式的化简求值,以及勾股定理的应用,关键是根据题意计算出BO、AO的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x-
=4,则x2+
的值为( )
| 1 |
| x |
| 1 |
| x2 |
| A、6 | B、16 | C、14 | D、18 |