题目内容
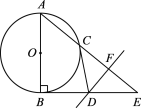
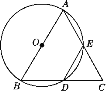
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.
(1)求证:△ABC为等边三角形.
(2)求DE的长.
【答案】(1)详见解析;(2)DE=1.
【解析】
(1)连接AD,利用直径所对的圆周角为直角及垂直平分线的性质得到相等的线段AB=AC,联立已知的AB=BC,即可证得△ABC是等边三角形;
(2)连接BE,利用直径所对的圆周角为直角,得到BE⊥AC,然后利用等腰三角形三线合一的性质得出E为AC的中点,继而利用三角形中位线的数量关系求得DE的长度.
(1)连接AD.
∵AB是⊙O的直径,∴∠ADB=90°.
∵点D是BC的中点,∴AD是线段BC的垂直平分线,∴AB=AC.
∵AB=BC,∴AB=BC=AC,∴△ABC为等边三角形.
(2)连接BE.
∵AB是直径,∴∠AEB=90°,∴BE⊥AC.
∵△ABC是等边三角形,∴AE=EC,即E为AC的中点.
∵D是BC的中点,∴DE为△ABC的中位线,∴DE=![]() AB=
AB=![]() ×2=1.
×2=1.

练习册系列答案
相关题目