题目内容
【题目】如图,某工厂要选一块矩形铁皮加工成一个底面半径为20 cm,高为![]() cm的圆锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少厘米的矩形铁皮,才能使所用材料最省?
cm的圆锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少厘米的矩形铁皮,才能使所用材料最省?
【答案】选长为90 cm,宽为60 cm的矩形铁皮,才能使所用材料最省.
【解析】
由于底面半径,高线,母线正好组成直角三角形,可由勾股定理求得母线长,则扇形的圆心角=底面周长×180÷(母线长×π),可在一长方形内画出一半径为60,圆心角为120°的扇形,有两种方案,由矩形和直角三角形的性质求得矩形长和宽,进而求得矩形的面积,比较即可得出用材料最省的方案.
∵圆锥形漏斗的底面半径为20cm,高为![]() cm,∴圆锥的母线长为R
cm,∴圆锥的母线长为R![]() 60(cm).
60(cm).
设圆锥的侧面展开图的圆心角为n°,则有![]() =2π×20,解得:n=120.
=2π×20,解得:n=120.
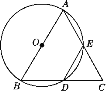
方案一:如图①,扇形的半径为60 cm,矩形的宽为60 cm,易求得矩形的长为![]() cm.
cm.
此时矩形的面积为![]() =
=![]() (cm2).
(cm2).
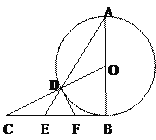
方案二:如图②,扇形与矩形的两边相切,有一边重合,易求得矩形的宽为60 cm,长为30+60=90(cm),此时矩形的面积为90×60=5 400(cm2).
∵![]() >5400,∴方案二所用材料最省,即选长为90 cm,宽为60 cm的矩形铁皮,才能使所用材料最省.
>5400,∴方案二所用材料最省,即选长为90 cm,宽为60 cm的矩形铁皮,才能使所用材料最省.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目