题目内容
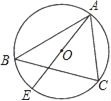
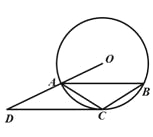
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,连结BD.
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由垂直的定义可得∠EBF=∠ADF=90°,于是得到∠C=∠BFE,从而证得△ABC≌△EBF;
(2)BD与⊙O相切,如图1,连接OB证得∠DBO=90°,即可得到BD与⊙O相切.
(1)∵∠ABC=90°,∴∠EBF=90°.
∵DF⊥AC,∴∠ADF=90°,∴∠C+∠A=∠A+∠AFD=90°,∴∠C=∠BFE.
在△ABC与△EBF中,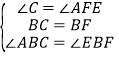 ,∴△ABC≌△EBF;
,∴△ABC≌△EBF;
(2)BD与⊙O相切.证明如下:
如图1,连接OB.
∵OB=OF,∴∠OBF=∠OFB.
∵∠ABC=90°,AD=CD,∴BD=CD,∴∠C=∠DBC.
∵∠C=∠BFE,∴∠DBC=∠OBF.
∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,∴∠DBO=90°,∴BD与⊙O相切.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目