题目内容
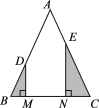
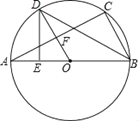
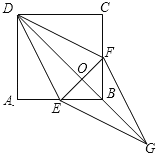
【题目】如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连结DB交EF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由.
【答案】(1)证明见解析
(2)四边形DEGF是菱形.理由见解析
【解析】
试题(1)由正方形的性质可得AD=CD,∠A=∠C=90°,然后利用“SAS”证明△ADE和△CDF全等,根据全等三角形对应边相等可得AE=CF;
(2)由(1)可得BE=BF,从而可得DE=DF,再根据到线段两端点距离相等的点在线段的垂直平分线可得BD为EF的中垂线,然后根据对角线互相垂直平分的四边形是菱形即可得证.
试题解析:(1)在正方形ABCD中,AD=CD,∠A=∠C=90°,
又∵∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴AE=CF;
(2)四边形DEGF是菱形.
理由如下:在正方形ABCD中,AB=BC,
∵AE=CF,
∴AB﹣AE=BC﹣CF,
即BE=BF,
∵△ADE≌△CDF,
∴DE=DF,
∴BD垂直平分EF,
又∵OG=OD,
∴四边形DEGF是菱形.

练习册系列答案
相关题目