Question

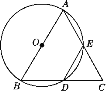
【题目】如图，在Rt△ABE中，∠B＝90°，以AB为直径的⊙O交AE于点C，CE的垂直平分线FD交BE于D，连接CD．

（1）判断CD与⊙O的位置关系，并证明；

（2）若AC·AE＝12，求⊙O的半径．

Answer 1

【答案】（1）CD与⊙O相切；（2）.

【解析】

（1）连接OC，由于FD是CE的垂直平分线，所以∠E=∠DCE，又因为∠A=∠OCA，∠A+∠E=90°，所以∠OCA+∠DCE=90°，所以CD与⊙O相切．

（2）连接BC，易知∠ACB=90°，所以△ACB∽ABE，所以，由于ACAE=12，所以AB=2. OA=AB=

（1）答：CD与⊙O相切．

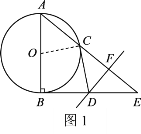
证明：如图1，连接OC．

∵ FD是CE的垂直平分线，

∴ DC=DE．

∴ ∠E=∠DCE．

∵ OA=OC，

∴ ∠A=∠OCA．

又∵在Rt△ABE中，∠B＝90°，

∴ ∠A+∠E=90°．

∴∠OCA+∠DCE＝90°．

∴ OC⊥CD．

∴ CD与⊙O相切．

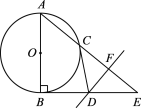
（2）如图2，连接BC．

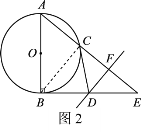
∵ AB是⊙O直径，

∴ ∠ACB=90°．

∴ △ACB∽△ABE．

∴ ．

∵ AC·AE＝12，

∴ ．

∴ ．

∴ ．