题目内容
【题目】如图,在ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
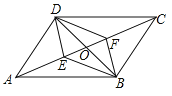
A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB
【答案】B
【解析】A选项:∵在平行四边形ABCD中,OA=OC,OB=OD,
若AE=CF,则OE=OF,
∴四边形DEBF是平行四边形;
B选项:若DE与AC不垂直,则满足AC上一定有一点DM=DE,同理有一点N使BF=BN,则四边形DEBF不一定是平行四边形,则选项错误;
C选项:∵在平行四边形ABCD中,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
若∠ADE=∠CBF,则∠DEB=∠FBO,
则△DOE和△BOF中,

∴△DOE≌△BOF,
∴DE=BF,
又∵DE∥BF,
∴四边形DEBF是平行四边形.故选项正确;
D选项:∵∠AED=∠CFB,
∴∠DEO=∠BFO,
∴DE∥BF,
在△DOE和△BOF中,
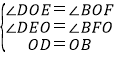
∴△DOE≌△BOF,
∴DE=BF,
∴四边形DEBF是平行四边形.故选项正确.
故选B.

练习册系列答案
相关题目