题目内容
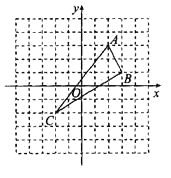
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,BE=3cm,AD=9cm.
求:(1)DE的长;
(2)若CE在△ABC的外部(如图),其它条件不变,DE的长是多少?

【答案】(1)DE= 6cm;(2)DE= 12cm.
【解析】试题分析:(1)由余角的性质,推出∠CBE=∠ECA,再依据全等三角形的判定定理“AAS”,推出△BEC和△CDA全等,然后即得BE=CD,CE=AD,再由BE=3cm,AD=9cm,结合图形即可推出DE=6cm,(2)根据余角的性质推出∠CBE=∠ACD,再依据全等三角形的判定定理“AAS”,推出△BEC和△CDA全等,然后即得BE=CD,CE=AD,再由BE=3cm,AD=9cm,结合图形即可推出DE=12cm.
试题解析:解:(1)∵∠ACB=90°,BE⊥CE,∴∠BCE+∠CBE=90°,∠BCE+∠ECA=90°,∴∠CBE=∠ECA,∠BEC=∠CDA.在△BEC和△CDA中,∵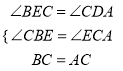 ,∴△BEC≌△CDA(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴CD=3cm,CE=9cm,∴DE=CE﹣CD=6cm.
,∴△BEC≌△CDA(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴CD=3cm,CE=9cm,∴DE=CE﹣CD=6cm.
(2)∵∠ACB=90°,BE⊥CE于E,AD⊥CE于D,∴∠BCE+∠CBE=90°,∠BCE+∠DCA=90°,∠BEC=∠CDA=90°,∴∠CBE=∠ACD.在△CBE和△ACD中,∵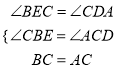 ,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴DE=CD+CE=BE+AD=12cm.
,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD.∵BE=3cm,AD=9cm,∴DE=CD+CE=BE+AD=12cm.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目