��Ŀ����
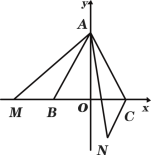
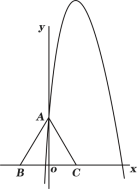
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У��ȱߡ�ABC�ı�BC��x���ϣ�A��0��3����B��![]() ��0������M��
��0������M��![]() ��0��Ϊx���ϵ�һ�����㣬����AM����AM�Ƶ�A��ʱ����ת60���õ�AN��
��0��Ϊx���ϵ�һ�����㣬����AM����AM�Ƶ�A��ʱ����ת60���õ�AN��
(1)��M����B�����ʱ������CN����֤����BAM�ա�CAN��
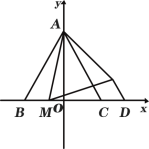
(2)��ͼ2����M���ڱ�BC��ʱ������N��ND//AC��x���ڵ�D������MN����![]() ������D������ꣻ
������D������ꣻ
(3)��ͼ3���Ƿ���ڵ�M��ʹ�õ�Nǡ����������![]() �ϣ�������ڣ������m��ֵ����������ڣ���˵�����ɣ�
�ϣ�������ڣ������m��ֵ����������ڣ���˵�����ɣ�
���𰸡�(1)��������(2)D(![]() ��0)��(3)���ڣ�
��0)��(3)���ڣ�![]() ��
��![]()
��������
��1�����ݵȱ������ε����ʡ���ת�����ʡ��ǵĺͲ�ɵ�![]() ��
��![]() ��
��![]() ���ٸ���ȫ�������ε��ж����ɵ�֤���ۣ�
���ٸ���ȫ�������ε��ж����ɵ�֤���ۣ�
��2����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ���ɵó�
���ɵó�![]() �ǵȱ������Σ��ٽ����֪�������ݵȱ������ε����ʡ���
�ǵȱ������Σ��ٽ����֪�������ݵȱ������ε����ʡ���![]() �ǵ�ֱ�������ε����ʵȿ��г�����
�ǵ�ֱ�������ε����ʵȿ��г�����![]() �ķ��̣����
�ķ��̣����![]() ������ô𰸣�
������ô𰸣�
��3���ɣ�2����֪��![]() ������Ϊ
������Ϊ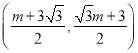 ������
������![]() ��������������߽���ʽ�ⷽ�̼��ɵý⣮
��������������߽���ʽ�ⷽ�̼��ɵý⣮
�⣺��1��֤������![]() �ǵȱ�������
�ǵȱ�������
��![]() ��
��![]()
�߽�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]()
��![]() ��
��![]()
��![]()
��![]()
����![]() ��
��![]() ��
��
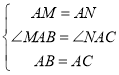
��![]() ��
��
��2����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ����ͼ��
����ͼ��

���ɣ�1����֪![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() �ǵȱ�������
�ǵȱ�������
��![]()
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��
��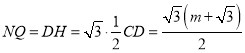
��![]()
��![]()
��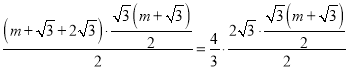
��![]()
��![]()
��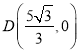 ��
��
��3���ɣ�2����֪��![]() ������Ϊ
������Ϊ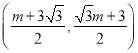
������![]() ǡ����������
ǡ����������![]() ��
��
��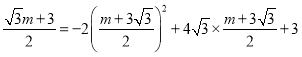
��![]() ��
��![]()
����ڵ�![]() ��ʹ�õ�
��ʹ�õ�![]() ǡ����������
ǡ����������![]() �ϣ���ʱ
�ϣ���ʱ![]() ��
��![]() ��
��

����Ŀ��ijˮ�����������ڣ������Ϊ10Ԫ/���ij��ˮ�����������ν��ۺ�ļ۸�Ϊ8.1Ԫ/��������ν��۵İٷ�����ͬ��
��1�������ˮ��ÿ�ν��۵İٷ��ʣ�
��2���ӵ�һ�ν��۵ĵ�1�����𣬵�x�죨xΪ���������ۼۡ��������������ķ��õ������Ϣ�����ʾ����֪����ˮ���Ľ���Ϊ4.1Ԫ/������۸�ˮ����x���죩������Ϊy��Ԫ������y��x��1��x��15��֮��ĺ�����ϵʽ��������ڼ���ʱ�����������
ʱ��x���죩 | 1��x��9 | 9��x��15 | x��15 |
�ۼۣ�Ԫ/� | ��1�ν��ۺ�ļ۸� | ��2�ν��ۺ�ļ۸� | |
������� | 80��3x | 120��x | |
�������ķ��ã�Ԫ�� | 40+3x | 3x2��64x+400 | |
��3���ڣ�2���������£���Ҫʹ��15�������ȣ�2����������������127.5Ԫ�����15���ڵ�14��ļ۸���������ɽ�����Ԫ��