题目内容
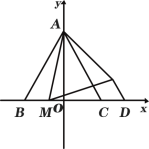
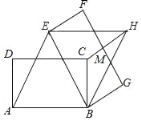
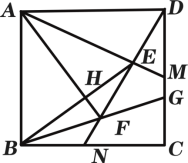
【题目】如图,在正方形ABCD中,AB=2,M为CD的中点,N为BC的中点,连接AM和DN交于点E,连接BE,作AH⊥BE于点H,延长AH与DN交于点F.连接BF并延长与CD交于点G,则MG的长度为__________.
【答案】![]()
【解析】
要求MG的长度,需要先求出CG的长,过F作PQ‖BC,连接MF,设出MQ,根据三角形相似分别表示出AP,PF,QF的长,根据勾股定理求出MQ的长,再根据△FGQ![]() △BGC求出CG的长即可求MG的长.
△BGC求出CG的长即可求MG的长.
如图:
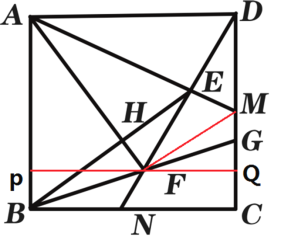
过点F作PQ平行于BC,分别交AB,DC于点P,点Q,连接MF;
∴∠APF=∠MQF=90°,
设MQ=x,则QD=x+1=AP,
∵在正方形ABCD中,AB=2,M为CD的中点,N为BC的中点,
∴MD=NC=![]() AB=1,
AB=1,
又AD=CD,
∴△AMD![]() △DNC,
△DNC,
∴∠NDC=∠DAM,
∴∠DEM=90°,
又∠MDE=∠FDQ,
∴△DEM![]() △FDQ,
△FDQ,
∴![]() ,
,
又∵∠DEM=90°,∠MDE=∠NDC,
∴△DEM![]() △DNC,
△DNC,
∴![]() ,
,
∴DE=2ME,
∵DM=1,由勾股定理可得:ME=![]() ,DE=
,DE= ![]() ,代入
,代入![]() ,
,
∴DQ=2QF,
∴QF=![]() ,
,
∴PF=2-QF= 2-![]() =
=![]() ,
,
在Rt△AMD中,AD=2,DM=1,
∴AM=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
整理得:![]() ,
,
解得:x=![]() ,x=-1(舍去),
,x=-1(舍去),
又∠FGQ=∠BGC,∠C=∠C,
∴△FGQ![]() △BGC,
△BGC,
∴![]() 即
即![]() ,
,
∵QC=CD-DQ=1-x,
∴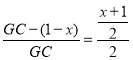 ,
,
解得:GC=![]() ,
,
∴MG=MC-GC=1-![]() =
=![]() ,
,
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的