Question

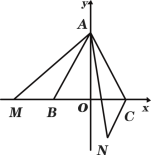
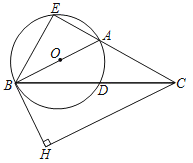
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D．延长CA交⊙O于点E，BH是⊙O的切线，作CH⊥BH．垂足为H．

（1）求证：BE＝BH；

（2）若AB＝5，tan∠CBE＝2，求BE的长．

Answer 1

【答案】（1）证明见解析；（2）4．

【解析】

（1）先根据圆的切线的性质可得，再根据平行线的判定与性质可得，然后根据等腰三角形的性质可得，从而可得，又根据圆周角定理可得，最后根据角平分线的性质即可得证；

（2）设，先根据正切函数值得出，再根据线段的和差可得，然后利用勾股定理即可得．

（1）BH是⊙O的切线

∴

又∵

∴

∴

又∵

∴

∴

是的角平分线

∵AB是直径

∴，即

∴；

（2）设

∵，即

∴

在中，由勾股定理得，即

解得或（不符题意，舍去）

故BE的长为4．