题目内容
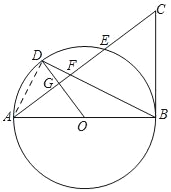
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

【答案】(1)证明见解析(2)![]()
【解析】
(1)由点G是AE的中点,根据垂径定理可知OD⊥AE,由等腰三角形的性质可得∠CBF=∠DFG,∠D=∠OBD,从而∠OBD+∠CBF=90°,从而可证结论;
(2)连接AD,解Rt△OAG可求出OG=3,AG=4,进而可求出DG的长,再证明△DAG∽△FDG,由相似三角形的性质求出FG的长,再由勾股定理即可求出FD的长.
(1)∵点G是AE的中点,
∴OD⊥AE,
∵FC=BC,
∴∠CBF=∠CFB,
∵∠CFB=∠DFG,
∴∠CBF=∠DFG
∵OB=OD,
∴∠D=∠OBD,
∵∠D+∠DFG=90°,
∴∠OBD+∠CBF=90°
即∠ABC=90°
∵OB是⊙O的半径,
∴BC是⊙O的切线;
(2)连接AD,
∵OA=5,tanA=![]() ,
,
∴OG=3,AG=4,
∴DG=OD﹣OG=2,
∵AB是⊙O的直径,
∴∠ADF=90°,
∵∠DAG+∠ADG=90°,∠ADG+∠FDG=90°
∴∠DAG=∠FDG,
∴△DAG∽△FDG,
∴![]() ,
,
∴DG2=AGFG,
∴4=4FG,
∴FG=1
∴由勾股定理可知:FD=![]() .
.

练习册系列答案
相关题目






