题目内容
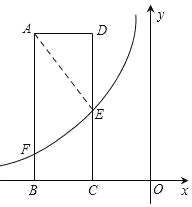
【题目】如图,矩形![]() 的两边
的两边![]() ,
,![]() 的长分别为3,8,且点
的长分别为3,8,且点![]() ,
,![]() 均在
均在![]() 轴的负半轴上,
轴的负半轴上,![]() 是
是![]() 的中点,反比例函数
的中点,反比例函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 交于点
交于点![]() .
.

(1)若点![]() 坐标为
坐标为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() ,则点
,则点![]() 的横坐标为______(用含
的横坐标为______(用含![]() 的代数式表示),点
的代数式表示),点![]() 的纵坐标为______,反比例函数的表达式为______.
的纵坐标为______,反比例函数的表达式为______.
【答案】(1)![]() ;(2)
;(2)![]() ,1,
,1,![]() .
.
【解析】
(1)根据矩形的性质,可得A,E的坐标,根据待定系数法即可求解;
(2)根据勾股定理,可得AE的长,根据线段的和差,可得FB,可得F的占比,根据待定系数法,可得m的值,即可求解.
解:(1)∵四边形![]() 是矩形,
是矩形,
∴![]() ,即
,即![]() 轴,
轴,
![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵点![]() 坐标为
坐标为![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
把点![]() 代入反比例函数
代入反比例函数![]() 得,
得,![]() ,∴
,∴![]() .
.
(2)如图,连接AE,∵点E的横坐标为a,BC=3
∴点F的横坐标为a-3,
又∵在Rt△ADE中,AE=![]()
∴AF=AE+2=7,BF=8-7=1
∴点F的纵坐标为1,
∴E(a,4),F(a-3,1)
∵反比例函数经过E,F
∴4a=1(a-3)
解得a=-1,
∴E(-1,4)
∴k=-4,
故反比例函数的解析式为![]()

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目