题目内容
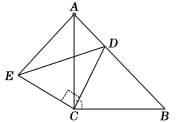
【题目】如图,已知E是正方形ABCD的边AB上一点,点A关于DE的对称点为F,若正方形ABCD的边长为1,且∠BFC=90°,则AE的长为___
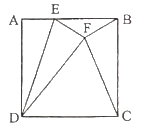
【答案】![]()
【解析】
延长EF交CB于M,连接DM,根据正方形的性质得到AD=DC,∠A=∠BCD=90°,由折叠的性质得到∠DFE=∠DFM=90°,通过Rt△DFM≌Rt△DCM,于是得到MF=MC.由等腰三角形的性质得到∠MFC=∠MCF由余角的性质得到∠MFC=∠MBF,于是求得MF=MB,根据勾股定理即可得到结论.
如图,
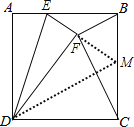
延长EF交CB于M,连接DM,
∵四边形ABCD是正方形,
∴AD=DC,∠A=∠BCD=90°,
∵将△ADE沿直线DE对折得到△DEF,
∴∠DFE=∠DFM=90°,
在Rt△DFM与Rt△DCM中,![]() ,
,
∴Rt△DFM≌Rt△DCM(HL),
∴MF=MC,
∴∠MFC=∠MCF,
∵∠MFC+∠BFM=90°,∠MCF+∠FBM=90°,
∴∠MFB=∠MBF,
∴MB=MC,
∴MF=MC=BM=![]() ,设AE=EF=x,
,设AE=EF=x,
∵BE2+BM2=EM2,
即(1-x)2+(![]() )2=(x+
)2=(x+![]() )2,
)2,
解得:x=![]() ,
,
∴AE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目