题目内容
若矩形ABCD能以某种方式分割成n个小矩形,使得每个小矩形都与原矩形ABCD相似,则此时我们称矩形ABCD可以自相似n分割,已知AB=1,BC=x(x≥1),
(1)若下图可以自相似2分割,请在图中画出分割草图,并求出x的值.
(2)若矩形ABCD可以自相似3分割,请画出两种不同分割的草图,并直接写出相应的x值.

(1)若下图可以自相似2分割,请在图中画出分割草图,并求出x的值.
(2)若矩形ABCD可以自相似3分割,请画出两种不同分割的草图,并直接写出相应的x值.

(1)∵是自相似2分割,
∴BF=FC=
BC,
根据相似矩形对应边成比例
=
,
∴x•
x=1,
解得x=
;
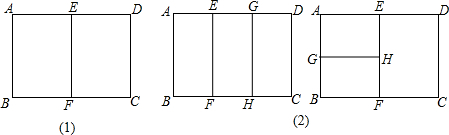
(2)如上图,EF,GH三等分矩形,则
=
,
∴x•
x=1,
解得x=
;
如上图,点G为AB中点,则
=
,
∴BF=
BC=
x,
又
=
,
∴BC•FC=CD•CD=1,
即x(x-
x)=1,
解得x=
.
∴BF=FC=
| 1 |
| 2 |
根据相似矩形对应边成比例
| BF |
| AB |
| AB |
| BC |
∴x•
| 1 |
| 2 |
解得x=
| 2 |

(2)如上图,EF,GH三等分矩形,则
| BF |
| AB |
| AB |
| BC |
∴x•
| 1 |
| 3 |
解得x=
| 3 |
如上图,点G为AB中点,则
| BG |
| AB |
| BF |
| BC |
∴BF=
| 1 |
| 2 |
| 1 |
| 2 |
又
| FC |
| CD |
| CD |
| BC |
∴BC•FC=CD•CD=1,
即x(x-
| 1 |
| 2 |
解得x=
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目