题目内容
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )


A.2 | B. | C.1 | D.2 |
B
作B点关于MN的对称点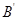 如图
如图 
连接 ,OB’∵∠AMN=30°B为AN弧的中点,∴∠AOB=60°∠NOB’=30°,故∠AOB’=90°,连接AB’则AB’与MN为所求P点,在Rt⊿AOB’中AB’为PA+PB的最小值即=
,OB’∵∠AMN=30°B为AN弧的中点,∴∠AOB=60°∠NOB’=30°,故∠AOB’=90°,连接AB’则AB’与MN为所求P点,在Rt⊿AOB’中AB’为PA+PB的最小值即=
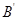 如图
如图 
连接
 ,OB’∵∠AMN=30°B为AN弧的中点,∴∠AOB=60°∠NOB’=30°,故∠AOB’=90°,连接AB’则AB’与MN为所求P点,在Rt⊿AOB’中AB’为PA+PB的最小值即=
,OB’∵∠AMN=30°B为AN弧的中点,∴∠AOB=60°∠NOB’=30°,故∠AOB’=90°,连接AB’则AB’与MN为所求P点,在Rt⊿AOB’中AB’为PA+PB的最小值即=

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 ▲ .
、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 ▲ .
 的代数式表示)
的代数式表示)
 是
是 的直径,
的直径, 为
为 ,则
,则 的度数为__________.
的度数为__________.

 中,
中, 点
点 在斜边
在斜边 上,以
上,以 为直径的
为直径的 与
与 相切于点
相切于点

 平分
平分
 ①求
①求
 是
是 的外接圆,
的外接圆, ,过点
,过点 作
作 ,交
,交 的延长线于点
的延长线于点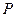 .
.
 是
是 ,求线段
,求线段