题目内容
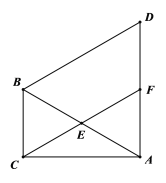
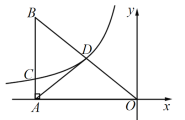
【题目】如图,函数![]() 的图象经过
的图象经过![]() 斜边
斜边![]() 的中点
的中点![]() ,与直角边
,与直角边![]() 相交于
相交于![]() ,连结
,连结![]() .若
.若![]() ,则
,则![]() 的周长为( )
的周长为( )
A.12B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
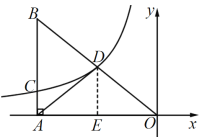
过点D作DE⊥AO于点E,设点D(a,b),根据点D在函数![]() 的图象上可得DE·OE=1,根据∠BAO=90°,点D为OB的中点,可得AD=DO=3,根据勾股定理可得DE2+OE2=DO2=9,进而可得(DE+OE)2=11,由此可求得DE+OE=
的图象上可得DE·OE=1,根据∠BAO=90°,点D为OB的中点,可得AD=DO=3,根据勾股定理可得DE2+OE2=DO2=9,进而可得(DE+OE)2=11,由此可求得DE+OE=![]() ,进而求得
,进而求得![]() ,最后根据相似三角形的性质即可求得答案.
,最后根据相似三角形的性质即可求得答案.
解:过点D作DE⊥AO于点E,
设点D(a,b),
则DE=b,OE=-a,
∵点D在函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴ab=-1,
∴DE·OE=-ab=1,
∵∠BAO=90°,点D为OB的中点,
∴AD=DO=3,
∴在Rt△DOE中,DE2+OE2=DO2=9,
∴(DE+OE)2= DE2+OE2+2 DE·OE
=9+2
=11
∴DE+OE=![]() (舍负)
(舍负)
∴![]() ,
,
∵点D为OB的中点,
∴DO=![]() ,
,
∵∠BAO=90°,DE⊥AO
∴∠BAO=∠DEO=90°,
∴DE∥AB,
∴△DEO∽△BAO,
∴![]() ,
,
∴![]()
![]()
![]() ,
,
故选:D.

练习册系列答案
相关题目