题目内容
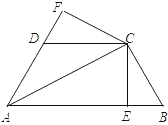
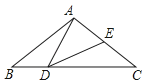
【题目】如图,在△ABC中,点D是边BC上的一点,点E是边AC上的一点,且AB=AC=DC,BD=CE,连接AD、DE.
(1)求证:△ADE是等腰三角形;
(2)若∠ADE=40°,请求出∠BAC的度数.
【答案】(1)证明见解析;(2)100°.
【解析】
(1)由“SAS”可证△ABD≌△DCE,可得AD=AE,即△ADE是等腰三角形;
(2)由全等三角形的性质可得∠BAD=∠EDC,由三角形内角和定理可求解.
证明:(1)∵AB=AC,
∴∠B=∠C,
在△ABD和△DCE中.
 ,
,
∴△ABD≌△DCE(SAS),
∴AD=DE,
∴△ADE是等腰三角形;
(2)∵△ABD≌△DCE,
∴∠BAD=∠EDC,
∴∠BAD+∠BDA=∠BDA+∠EDC=180°﹣∠ADE=140°,
∴在△ABD中,∠B=180°﹣140°=40°,
∴∠C=∠B=40°,
∴∠BAC=180°﹣40°﹣40°=100°.

【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
【题目】下表是随机抽取的某公司部分员工的月收入资料.
月收入/元 | 45000 | 18000 | 10000 | 5500 | 5000 | 3400 | 3000 | 2000 |
人数 | 1 | 1 | 1 | 3 | 6 | 1 | 11 | 2 |
(1)请计算样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;并指出谁的推断比较科学合理,能直实地反映公司全体员工月收入水平.