题目内容
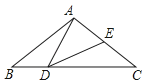
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
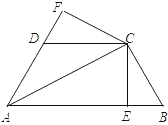
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求AC的长.
【答案】(1)见解析;(2)AC的长为17.
【解析】
(1)首先根据垂线的意义得出∠CFD=∠CEB=90°,然后根据角平分线的性质得出CE=CF,即可判定Rt△BCE≌Rt△DCF;
(2)首先由(1)中全等三角形的性质得出DF=EB,然后判定Rt△AFC≌Rt△AEC,得出AF=AE,构建方程得出CF,再利用勾股定理即可得出AC.
(1)∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴∠CFD=90°,∠CEB=90°(垂线的意义)
∴CE=CF(角平分线的性质)
∵BC=CD(已知)
∴Rt△BCE≌Rt△DCF(HL)
(2)由(1)得,
Rt△BCE≌Rt△DCF
∴DF=EB,设DF=EB=x
∵∠CFD=90°,∠CEB=90°,
CE=CF,AC=AC
∴Rt△AFC≌Rt△AEC(HL)
∴AF=AE
即:AD+DF=AB﹣BE
∵AB=21,AD=9,DF=EB=x
∴9+x=21﹣x解得,x=6
在Rt△DCF中,
∵DF=6,CD=10
∴CF=8
∴Rt△AFC中,AC2=CF2+AF2=82+(9+6)2=289
∴AC=17
答:AC的长为17.

练习册系列答案
相关题目