题目内容
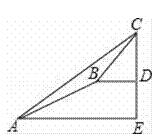
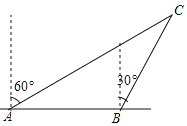
【题目】如图,某渔船向正东方向以12海里/时的速度航行,在A处测得岛C在北偏东的60°方向,1小时后渔船航行到B处,测得岛C在北偏东的30°方向,已知该岛周围10海里内有暗礁.
(1)B处离岛C有多远?
(2)如果渔船继续向东航行,有无触礁危险?
【答案】(1)B处离岛C有12海里;(2)没有触礁危险.
【解析】
(1) 过C作CO垂直AB,,通过证明∠ACB=∠CAB=30,即可求出CB的长;
(2)求出点C到AB的距离是否大于10,如果大于10则无触礁危险,反之则有.
(1)过C作CO垂直AB,
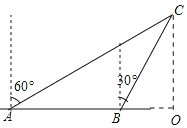
CO为渔船向东航行到C道最短距离
∵在A处测得岛C在北偏东的60°
∴∠CAB=30°
又∵B处测得岛C在北偏东30°,
∴∠CBO=60°,∠ABC=120°,
∴∠ACB=∠CAB=30°,
∴AB=BC=12×1=12(海里)(等边对等角);
(2)∵CO⊥AB,∠CBO=60°
∴CO=6![]() (海里)>10(海里)
(海里)>10(海里)
故如果渔船继续向东航行,没有触礁危险

练习册系列答案
相关题目