Question

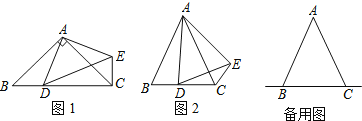
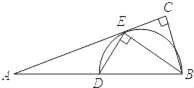
【题目】如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，点D在AB边上且DE⊥BE．

（1）判断直线AC与△DBE外接圆的位置关系，并说明理由；

（2）若AD=6，AE=6，求BC的长．

Answer 1

【答案】（1）直线AC与△DBE外接圆相切．（2）BC=4．

【解析】

（1）取BD的中点O，连接OE，证明∠OEB=∠CBE后可得OE⊥AC；

（2）设OD=OE=OB=x，利用勾股定理求出x的值，再证明△AOE∽△ABC，利用线段比求解．

（1）直线AC与△DBE外接圆相切．

理由：∵DE⊥BE

∴BD为△DBE外接圆的直径

取BD的中点O（即△DBE外接圆的圆心），连接OE

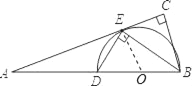
∴OE=OB

∴∠OEB=∠OBE

∵BE平分∠ABC

∴∠OBE=∠CBE

∴∠OEB=∠CBE

∵∠CBE+∠CEB=90°

∴∠OEB+∠CEB=90°，即OE⊥AC

∴直线AC与△DBE外接圆相切；

（2）设OD=OE=OB=x

∵OE⊥AC

∴（x+6）2﹣（6）2=x2

∴x=3

∴AB=AD+OD+OB=12

∵OE⊥AC

∴△AOE∽△ABC

∴,即

∴BC=4．