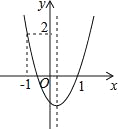题目内容
【题目】(1)探究新知:

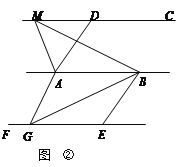
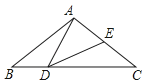
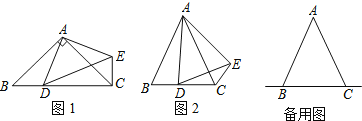
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.试判断△ABM与△ABN的面积是否相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
(2)结论应用:
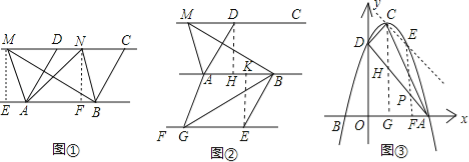
如图③,抛物线![]() 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线![]() 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?若存在,请求出此时点E的坐标,若不存在,请说明理由.


【答案】(1)①证明见解析.②相等;理由见解析.(2)存在.
【解析】
试题(1)①由于CD∥AB,所以△ABM和△ABN中,AB边上的高相等,则两个三角形是同底等高的三角形,所以它们的面积相等;
②分别过D、E作AB的垂线,设垂足为H、K;通过证△DAH≌△EBK,来得到DH=KE;则所求的两个三角形是同底等高的三角形,由此得证;
(2)根据A、C的坐标,即可求得抛物线的解析式,进而可求出A、D的解析式;用待定系数法可确定直线AD的解析式;假设存在符合条件的E点,过C作CD⊥x轴于D,交直线AD于H;过E作EF⊥x轴于F,交直线AD于P;根据抛物线的对称轴方程及直线AD的解析式,易求得H点的坐标,即可得到CH的长;设出E点横坐标,根据直线AD和抛物线的解析式,可表示出P、E的纵坐标,即可得到PE的长;根据(1)题得到的结论,当PE=CH时,所求的两个三角形面积相等,由此可列出关于E点横坐标的方程,从而求出E点的坐标.(需注意的是E点可能在直线AD的上方或下方,这两种情况下PE的表达式会有所不同,要分类讨论)
试题解析:证明:(1)①分别过点M,N作ME⊥AB,NF⊥AB,垂足分别为点E,F
∵AD∥BC,AD=BC,
∴四边形ABCD为平行四边形;
∴AB∥CD;
∴ME=NF;
∵S△ABM=![]() ,S△ABN=
,S△ABN=![]() ,
,
∴S△ABM=S△ABN
②解:相等;理由如下:分别过点D,E作DH⊥AB,EK⊥AB,垂足分别为H,K;
则∠DHA=∠EKB=90°;
∵AD∥BE,
∴∠DAH=∠EBK;
∵AD=BE,
∴△DAH≌△EBK;
∴DH=EK;(2分)
∵CD∥AB∥EF,
∴S△ABM=![]() ,S△ABG=
,S△ABG=![]() ,
,
∴S△ABM=S△ABG;
解:(2)存在.
因为抛物线的顶点坐标是C(1,4),
所以,可设抛物线的表达式为y=a(x-1)2+4;
又因为抛物线经过点A(3,0),
所以将其坐标代入上式,得0=a(3-1)2+4,解得a=-1;
∴该抛物线的表达式为y=-(x-1)2+4,
即y=-x2+2x+3;
∴D点坐标为(0,3);
设直线AD的表达式为y=kx+3,
代入点A的坐标,得0=3k+3,解得k=-1;
∴直线AD的表达式为y=-x+3;
过C点作CG⊥x轴,垂足为G,交AD于点H;则H点的纵坐标为-1+3=2;
∴CH=CG-HG=4-2=2;
设点E的横坐标为m,则点E的纵坐标为-m2+2m+3;
过E点作EF⊥x轴,垂足为F,交AD于点P,则点P的纵坐标为3-m,EF∥CG;
由﹙1﹚可知:若EP=CH,则△ADE与△ADC的面积相等;
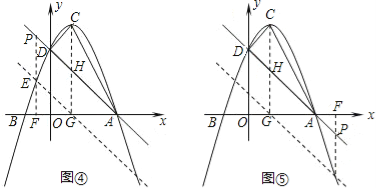
①若E点在直线AD的上方,
则PF=3-m,EF=-m2+2m+3,
∴EP=EF-PF=-m2+2m+3-(3-m)=-m2+3m;
∴-m2+3m=2,
解得m1=2,m2=1;
当m=2时,PF=3-2=1,EF=1+2=3;
∴E点坐标为(2,3);
同理当m=1时,E点坐标为(1,4),与C点重合;
②若E点在直线AD的下方,
则PE=(3-m)-(-m2+2m+3)=m2-3m;
∴m2-3m=2,
解得![]() ,
,![]() ;
;
当![]() 时,E点的纵坐标为
时,E点的纵坐标为![]() ;
;
当![]() 时,E点的纵坐标为
时,E点的纵坐标为![]() ;
;
∴在抛物线上存在除点C以外的点E,使得△ADE与△ACD的面积相等,E点的坐标为E1(2,3);E2(![]() ,
,![]() );E3(
);E3(![]() ,
,![]() ).
).

 小学期末标准试卷系列答案
小学期末标准试卷系列答案