Question

如图，抛物线经过A（-1，0），B（5，0），C（0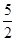，?）三点．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．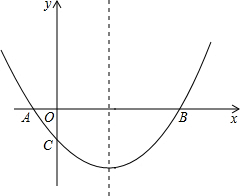

Answer 1

（1）抛物线的解析式为：；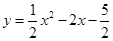
（2）P（2，-）；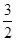
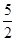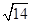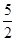(3)存在，符合条件的点N的坐标为（4，-），（2+，）或（2-，）.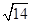

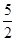解析试题分析：（1）设抛物线的解析式为y=ax²+bx+c（a≠0），再把A（-1，0），B（5，0），C（0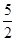，?）三点代入求出a、b、c的值即可；
（2）因为点A关于对称轴对称的点B的坐标为（5，0），连接BC交对称轴直线于点P，求出P点坐标即可；
（3）分点N在x轴下方或上方两种情况进行讨论．
（1）设抛物线的解析式为y=ax²+bx+c（a≠0），
∵A（-1，0），B（5，0），C（0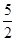，?）三点在抛物线上，
∴，
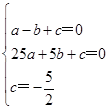解得 ．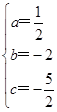
∴抛物线的解析式为：；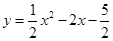
（2）∵抛物线的解析式为：，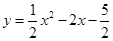
∴其对称轴为直线，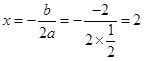
连接BC，如图1所示，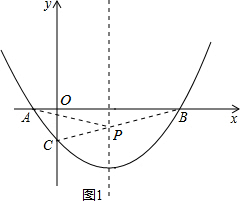

∵B（5，0），C（0，-），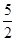
∴设直线BC的解析式为y=kx+b（k≠0），
∴ ，
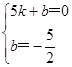解得 ，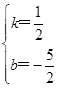
∴直线BC的解析式为，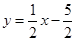
当x=2时，y=1-=-，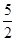
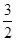∴P（2，-）；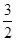
（3）存在．
如图2所示，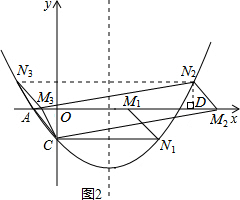

①当点N在x轴下方时，；
∵抛物线的对称轴为直线x=2，C（0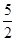，-），∴N₁（4，-）
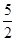②当点N在x轴上方时，
如图，过点N₂作N₂D⊥x轴于点D，
在△AN₂D与△M₂CO中，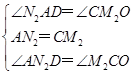
 ，
∴△AN₂D≌△M₂CO（ASA），
∴N₂D=OC=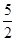，即N₂点的纵坐标为．
∴，
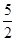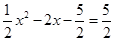解得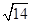x=2+或x=2-，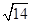
∴N₂（2+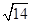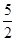，），N₃（2-，）．
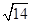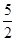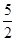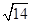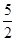综上所述，符合条件的点N的坐标为（4，-），（2+，）或（2-，）．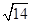
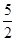考点：二次函数综合题．