题目内容
如图,已知抛物线y=﹣ x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
(1)y=-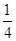 x2+
x2+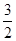 x+4,x=3;(2)C(0,4);y=?
x+4,x=3;(2)C(0,4);y=? x+4.(3)Q1(3,0),Q2(3,4+
x+4.(3)Q1(3,0),Q2(3,4+ ),Q3(3,4-
),Q3(3,4- ).
).
解析试题分析:(1)利用待定系数法求出抛物线解析式,利用配方法或利用公式x=?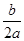 求出对称轴方程;
求出对称轴方程;
(2)在抛物线解析式中,令x=0,可求出点C坐标;令y=0,可求出点B坐标.再利用待定系数法求出直线BD的解析式;
(3)本问为存在型问题.若△ACQ为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解.
(1)∵抛物线y=-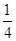 x2+bx+4的图象经过点A(-2,0),
x2+bx+4的图象经过点A(-2,0),
∴-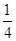 ×(-2)2+b×(-2)+4=0,
×(-2)2+b×(-2)+4=0,
解得:b=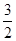 ,
,
∴抛物线解析式为 y=-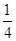 x2+
x2+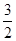 x+4,
x+4,
又∵y=-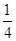 x2+
x2+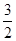 x+4=-
x+4=-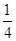 (x-3)2+
(x-3)2+ ,
,
∴对称轴方程为:x=3.
(2)在y=-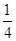 x2+
x2+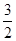 x+4中,令x=0,得y=4,
x+4中,令x=0,得y=4,
∴C(0,4);
令y=0,即-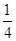 x2+
x2+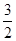 x+4=0,整理得x2-6x-16=0,解得:x=8或x=-2,
x+4=0,整理得x2-6x-16=0,解得:x=8或x=-2,
∴A(-2,0),B(8,0).
设直线BC的解析式为y=kx+b,
把B(8,0),C(0,4)的坐标分别代入解析式,得: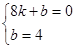 ,
,
解得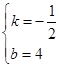 ,
,
∴直线BC的解析式为:y=? x+4.
x+4.
∵抛物线的对称轴方程为:x=3,
可设点Q(3,t),则可求得:
AC= ,
,
AQ= ,
,
CQ= .
.
i)当AQ=CQ时,有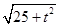 =
=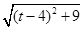 ,
,
25+t2=t2-8t+16+9,
解得t=0,
∴Q1(3,0);
ii)当AC=AQ时,有
t2=-5,此方程无实数根,
∴此时△ACQ不能构成等腰三角形;
iii)当AC=CQ时,有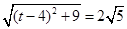 ,
,
整理得:t2-8t+5=0,
解得:t=4± ,
,
∴点Q坐标为:Q2(3,4+ ),Q3(3,4-
),Q3(3,4- ).
).
综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+ ),Q3(3,4-
),Q3(3,4- ).
).
考点:二次函数综合题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 时,求点E的坐标;
时,求点E的坐标;
 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
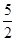 )三点.
)三点.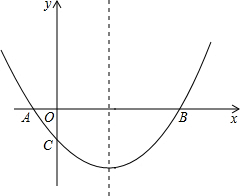

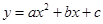 交
交 轴于A、B两点(点A在点B左侧),与
轴于A、B两点(点A在点B左侧),与 轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线
轴交于点C,点A、C的坐标分别为(-3,0),(0,3),对称轴直线 交
交 ,,求点P的坐标;
,,求点P的坐标;
 x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.